Day: December 4, 2010

Relatywistyczne składanie prędkości

Posted on by arkajad

W notce Szczególna teoria względności – Cz. 1 zapisaliśmy ogólną transformację Lorentza w postaci

x^\mu=\Lambda^\mu_{\mu'}x^{\mu'}.

Transformacja odwrotna zapisywana jest jako

x^{\mu'}=\Lambda^{\mu'}_{\mu}x^{\mu}.

Macierz \Lambda=\{\Lambda^{\mu'}_{\mu}\} winna przy tym spełniać warunek

\Lambda^T\eta\Lambda=\eta

gdzie \eta jest macierzą definiującą interwał czasoprzestrzenny geometrii przestrzeni Minkowskiego:

\eta=\begin{pmatrix} -1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}

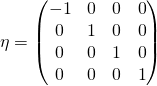
W notce “Szczególne transformacje Lorentza” zajęliśmy się najprostszym ciekawym przypadkiem, gdy jeden układ odniesienia porusza się względem drugiego z prędkością v wzdłuż jednej osi – była to oś x. Wtedy

x{^0}'=\gamma(x^0-\beta x)
x'=\gamma (x-\beta x^0)
y'=y
z'=z.

gdzie

\gamma=1/\sqrt{1-\beta^2},\quad \beta=v/c.

Macierz \Lambda ma dla takich transformacji postać:

\Lambda=\begin{pmatrix}\gamma&-\beta\gamma&0&0\\-\beta\gamma&\gamma&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}

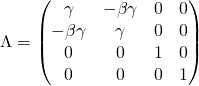
Przyjrzyjmy się tej nietrywialnej lewej górnej klatce naszej macierzy. Dla klatki tej warunek \Lambda^T\eta\Lambda=\eta daje

-(\Lambda^0'_0)^2+(\Lambda^0'_1)^2=-1
-(\Lambda^1'_0)^2+(\Lambda^1'_1)^2=1

W naszym przypadku \Lambda^0'_0=\Lambda^1'_1=\gamma, \Lambda^0'_1=\Lambda^1'_0=-\beta\gamma i warunki te są automatycznie spełnione – jak łatwo się przekonać – wprost z definicji \gamma.

Zapiszmy nasze warunki w nieco ładniejszej dla oka postaci:

(\Lambda^0'_0)^2-(\Lambda^0'_1)^2=1
(\Lambda^1'_1)-(\Lambda^1'_0)^2=1

Przypominają one znany wzór trygonometryczny:

\cos^2\alpha+\sin^2\alpha=1

tyle, że w transformacjach Lorentza mamy minus zamiast plusa. Istnieje wszak nieperiodyczna wersja funkcji trygonometrycznych, tzw. funkcje hiperboliczne.

Funkcje hiperboliczne

Zacząć tu trzeba od funkcji wykładniczej e^x. Jej wykres ma dość dobrze znaną postać:

Exponential function
Funkcja wykładnicza

Przy pomocy funkcji wykładniczej tworzymy hiperboliczny odpowiednik sinusa:

Hyperbolic sinus
Sinus hiperboliczny

Definicja jest prosta:

\sinh(x)=\frac{e^x-e^{-x}}{2}

Podobnie jak zwykły sinus jest to funkcja nieparzysta: \sinh(-x)=-\sinh(x).

Dalej mamy cosinus hiperboliczny

\cosh(x)=\frac{e^x+e^{-x}}{2}

Hyperbolic cosinus
Cosinus hiperboliczny

Ten jest funkcją parzystą: \cosh(-x)=\cosh(x).

Wreszcie mamy (nieparzysty) tangens hiperboliczny:

\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}

o wykresie

Hyperbolic tangent
Tangens hiperboliczny

Jak się łatwo przekonać wprost z definicji, dla funkcji hiperbolicznych mamy:

\cosh^2\alpha-\sinh^2\alpha=1

zatem dokładnie tak jak to jest w naszej szczególnej transformacji Lorentza. Sugeruje nam ta obserwacja, że warto wprowadzić, miast wielkości \beta=v/c nową wielkość \alpha tak, by było:

\gamma=\cosh\,\alpha

\beta\gamma=\sinh\,\alpha

Wtedy \beta=\frac{\beta\gamma}{\gamma}=\tanh\,\alpha. Macierz szczególnej transformacji Lorentza w dwóch wymiarach ma wtedy wyjątkowo prostą postać:

\Lambda(\alpha)=\begin{pmatrix}\cosh\,\alpha&-\sinh\,\alpha\\-\sinh\,\alpha&\cosh\,\alpha\end{pmatrix}

Łatwo możemy wyrazić \alpha przez \beta

\alpha=\mathrm{artgh}(\beta)

gdzie \mathrm{artgh} jest funkcją odwrotną do tangensa hiperbolicznego, o wykresie

inverse hyperbolic tangent
Area tangens hiperboliczny

Dodawanie prędkości

Podczas gdy \beta=v/c zmienia sie w zakresie -1<\beta<1 to \alpha ma zakres -\infty<\alpha<\infty.

Wprowadzenie \alpha miast \beta ma jeszcze jedną przyjemną własność, a wiąże się ona z relatywistycznym prawem składania prędkości. Przypuśćmy, że mamy trzy układy odniesienia: S,S’,S”, przy czym S’ porusza się względem S z prędkością \beta zaś S” porzusza się względem S’ z prędkością \beta'. Z jaką prędkością będzie się poruszał S” względem S? Otóż, bynajmniej nie z prędkością \beta+\beta'.  Wymnażając macierze przekształceń Lorentza:

\Lambda(\alpha)=\begin{pmatrix}\cosh(\alpha)&-\sinh(\alpha)\\-\sinh(\alpha)&\cosh(\alpha)\end{pmatrix}

\Lambda(\alpha')=\begin{pmatrix}\cosh(\alpha')&-\sinh(\alpha')\\-\sinh(\alpha')&\cosh(\alpha')\end{pmatrix}

przekonujemy się łatwo, że

\Lambda(\alpha)\Lambda(\alpha')=\Lambda(\alpha')\Lambda(\alpha)=\Lambda(\alpha+\alpha')

Przy składaniu prędkości dodają się więc parametry \alpha, zaś \beta zależy od \alpha w sposób nieliniowy – dla bet dodawania nie będzie! A co będzie?

Szperając w Wikipedii znaleźć możemy następującą tożsamość dla funkcji tanh:

\tanh(\alpha+\alpha')=\frac{\tanh(\alpha)+\tanh(\alpha')}{1+\tanh(\alpha)\tanh(\alpha')}

Podstawiając \beta''=\tanh(\alpha+\alpha'),\,\beta'=\tanh(\alpha'),\,\beta=\tanh(\alpha) otrzymujemy relatyvistyczne prawo skaładania prędkości:

\beta''=\frac{\beta+\beta'}{1+\beta\beta'}

lub przy pomocy prędkości, pamietająć, że \beta =v/c

v''=\frac{v+v'}{1+ \frac{vv'}{c^2}}

Jeśli więc np. \beta=0.75c, \beta'=0.75c to złożenie tych dwóch prędkości nie daje bynajmniej 1.5c. Miast tego otrzymujemy

\beta''=\frac{0.75+0.75}{1+(0.75)^2}=0.96c

Składając relatywistycznie prędkości mniejsze od prędkości światła nigdy prędkości światła nie przekroczymy.