Niniejszy post jest małą trnasformacją mojej notki Szczególne przekształcenia Lorentza w Salon24. Zmieniłem niewiele – użyłem kodu Latexa miast wklejania obrazków, to i owo wyprostowałem. Chcę jednak mieć całą konieczną matematykę w jednym miejscu.
Wprowadźmy oznaczenie 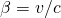 dla oznaczenia prędkości jednego układu odniesienia względem drugiego. Ponieważ w STW prędkość
dla oznaczenia prędkości jednego układu odniesienia względem drugiego. Ponieważ w STW prędkość  jest mniejsza od prędkości światła, zatem zawsze
jest mniejsza od prędkości światła, zatem zawsze  Wprowadza się też zazwyczaj skrót
Wprowadza się też zazwyczaj skrót 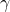 dla oznaczenia:
dla oznaczenia:
Najprostsza transformacja Lorentza, to transformacja w dwóch wymiarach, gdy mamy tylko współrzędne 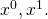 Ma wtedy znaną powszechnie postać:
Ma wtedy znaną powszechnie postać:
W postaci jawnej, przy użyciu ![]() oraz
oraz ![]() :
:
![]()
![]()
Przekształcenie odwrotne ma dokładnie tą samą postać, tyle, że trzeba zamienić  na
na 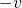 . Zauważmy, że
. Zauważmy, że 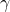 sie przy tym nie zmienia.
sie przy tym nie zmienia.
Przekształcenie to możemy przedstawić w postaci graficznej. Zazwyczaj wybiera się w tym celu osie 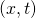 prostopadłe do siebie – bo tak jesteśmy przyzwyczajeni. Ale nowe osie
prostopadłe do siebie – bo tak jesteśmy przyzwyczajeni. Ale nowe osie 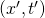 już nie będą do siebie prostopadłe. Nic dziwnego, bowiem prostopadłość euklidesowa nie jest prostopadłością przestrzeni Minkowskiego. Oto typowy grafik transformacji szczególnej Lorentza.
już nie będą do siebie prostopadłe. Nic dziwnego, bowiem prostopadłość euklidesowa nie jest prostopadłością przestrzeni Minkowskiego. Oto typowy grafik transformacji szczególnej Lorentza.
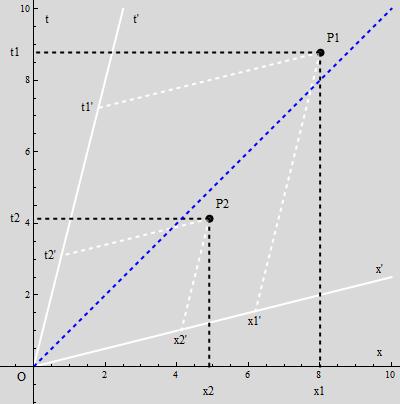
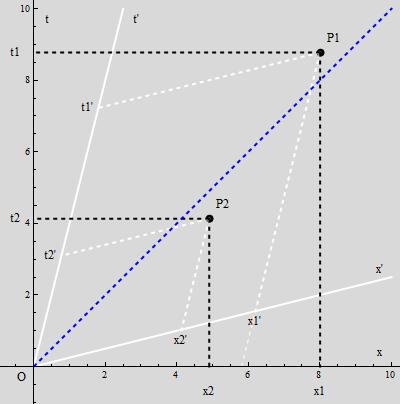
Na tym obrazku – gdzie przyjąłem umownie prędkość światła 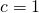 – względem układu nieprimowanego S, układ primowany, nazwijmy go S’, porusza się z prędkością 0.25c – .(Można np. sobie pomyśleć, że na osi t jednostką są lata, a na osi x jednostką są lata świetlne). Mamy też dwa zdarzenia P1 i P2. Zdarzenia te mają w układzie S współrzędne
– względem układu nieprimowanego S, układ primowany, nazwijmy go S’, porusza się z prędkością 0.25c – .(Można np. sobie pomyśleć, że na osi t jednostką są lata, a na osi x jednostką są lata świetlne). Mamy też dwa zdarzenia P1 i P2. Zdarzenia te mają w układzie S współrzędne 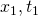 i
i  odpowiednio. W układzie S’ współrzędne te są inne, mianowicie
odpowiednio. W układzie S’ współrzędne te są inne, mianowicie 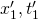 i
i 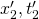 . Niebieską przerywaną linią narysowałem historię promienia świetlnego wysłanego z początku O uładu w zerowej chwili. Linia ta ma równanie
. Niebieską przerywaną linią narysowałem historię promienia świetlnego wysłanego z początku O uładu w zerowej chwili. Linia ta ma równanie 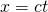 (pamiętajmy, że tutaj c=1, zatem
(pamiętajmy, że tutaj c=1, zatem 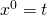 ). W chwili zerowej początki obu układów są identyczne. Widać, że punkt P1 połączony jest z O interwałem czasopodobnym, można więc z O wysłać sygnał z prędkością mniejszą od c i sygnał ten dotrze do P1. Natomiast P2 połączony jest z O interwałem przestrzennopodobnym. Połączenie zdarzeń O i P2 wymagałoby sygnału o prędkości ponadświetlnej. Zdarzenia P1 i P2, jak widać z rysunku, połączone są interwałem czasopodobnym. Czym szybciej układ S’ porusza się względem S, tym bardziej – na tym obrazku – jego osie będą się “składać”. W granicy
). W chwili zerowej początki obu układów są identyczne. Widać, że punkt P1 połączony jest z O interwałem czasopodobnym, można więc z O wysłać sygnał z prędkością mniejszą od c i sygnał ten dotrze do P1. Natomiast P2 połączony jest z O interwałem przestrzennopodobnym. Połączenie zdarzeń O i P2 wymagałoby sygnału o prędkości ponadświetlnej. Zdarzenia P1 i P2, jak widać z rysunku, połączone są interwałem czasopodobnym. Czym szybciej układ S’ porusza się względem S, tym bardziej – na tym obrazku – jego osie będą się “składać”. W granicy 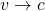 złożą się w jedną prostą – tę narysowaną na niebiesko i reprezentującą promień świetlny.
złożą się w jedną prostą – tę narysowaną na niebiesko i reprezentującą promień świetlny.
Mógłbym zrobić inaczej – mógłbym osie układu S’ narysować jako prostopadłe. Wtedy osie układu S narysowałbym jako rozchylone.
Jeszcze trochę opisu do rysunku. Linia pionowa z O to historia początku układu S. Linia ukośna wiodąca z O(=O’) ku t’ – to historia początku układu S’. Linia pozioma z O – to “zdarzenia jednoczesne z O patrząc z S“. Linia ukośna z O ku x’, to “zdarzenia jednoczesne z O patrząc z S‘ “.
Relatywistyczne skrócenie
Zanim przyjrzymy się jak odczytać z naszego obrazka relatywistyczne skrócenie, podam dane liczbowe, których użyłem przy jego produkcji. v=0.25, stąd ![]() .
.
Współrzędne zdarzenia P1 w układzie S: t1 = 8.77876, x1=8.00417 Współrzędne zdarzenia P1 w układzie S’: t1′ = 7, x1′ = 6
Współrzędne zdarzenia P2 w układzie S: t2 = 4.13118, x2 = 4.90578 Współrzędne zdarzenia P2 w układzie S’: t2′ = 3, x2′ = 4. Przyjrzyjmy się obrazkowi raz jeszcze, tyle, że pociągnijmy linię przerywaną od punktu oznaczonego symbolem x1’w dół, do poziomej osi x. Można porachować, że przetnie ona oś x dla x = 5.80948.
Jaka temu faktowi towarzyszy interpretacja? Grafik czasoprzestrzenny, jak powyżej, to jedna rzecz, a zdanie sobie sprawy z tego co się dzieje – to rzecz druga. Przestrzeń w naszym prostym przypadku, jest jednowymiarowa. Układ odniesienia to zwykła linijka. Drugi układ odniesienia – to druga linijka. Jedna linijka przesuwa się z prędkością 1/4 prędkości światła wzdłuż drugiej linijki. (Nie jest to prędkość zawrotna, bowiem prędkość transmisji sygnałów w typowych liniach przesyłowych wynosi ok. 3/4 prędkości światła). Na obrazku wygląda to jakoś tak:

Dla obserwatora w układzie S’, w chwili (dla niego) 0 jego linijka jest reprezentowana na Rys. 2 przez białą linię 0x’. W jego chwili t1′ jest to biała linia t1’P1. Punkt jego linijki reprezentujący jego współrzędną zdarzenia P1 to 6. Zaznaczył sobie ten punkt. Linia ukośna łącząca x1′ z P1 to historia tego zaznaczonego punktu – który to punkt porusza się względem S z prędkością 0.25c. Gdy jednak obie linijki miały wspólny początek (z punktu widzenia S i S’), to jest w O, punkt ten miał współrzędną 5.80948 w układzie S. Zatem poruszająca się linijka wygląda na skróconą gdy ogląda ją obserwator w S. Skrócenie to przedstawione jest na obrazku przez odstęp pomiędzy x=6 a punktem przecięcia przerywanej linii z osią x. Można się łatwo przekonać, że 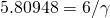 . Stąd
. Stąd 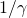 nazywa się czynnikiem skrócenia Lorentza.
nazywa się czynnikiem skrócenia Lorentza.


errata
powszechnie postać: x0 ->
powszechnie postać: x0′
PS
Jak skasowywać własny komentarz?
Dawałem sup 0 sup.
W podglądzie wychodziło ładnie u góry w indeksie.
W efekcie wyszło zwykłe :(
Używaj [ math ]x^0[ /math ] (latex), bez spacji w nawiasach). Kasować własnych komentarzy się tu nie da. Trzeba mnie prosić.