Day: January 16, 2017

Jacobi amplitude- realism or cubism

Posted on by arkajad

Jacobi amplitude function we know from the previous post Jacobi Elliptic SN – The case of inverted modulus. Here we will continue this subject.

We define Jacobi incomplete elliptic integral of the first kind F(\phi,m) as

(1)   \begin{equation*} F(\phi,m)=\int_0^\phi\frac{d\theta}{\sqrt{1-m\sin^2\theta}}.\end{equation*}

Something must be said about the domain of this function, that is about the ranges of values of \phi and m for which the definition above makes sense. If we check Wikipedia’s entry Elliptic integral, we realize that Wikipedia is silent about this subject.

So, let’s go to Wolfram’s site Introduction to the incomplete elliptic integrals. There we find that Wolfram seems to restrict the allowed values of m to 0<m<1.

But if we go to Matlab’s site, we find that Matlab has no inhibitions at all about the allowed values of m:

So, we try Wolfram’s Mathematica to plot F(\pi/3,m) for the same range of m as in Matlab’s plot. We get

That is reasonable. Since \sin^2\pi/3=3/4, the limit of the allowed values of m should occur when m\sin^2\pi/3=1, that is for m=4/3=1.3333, and this is exactly what happens. Thus the domain of F consists of those \phi and m for which the integral is still finite, that is as long as m\sin^2\theta in the integrand stays away from 1. The range of F is always the whole real axis. Jacobi amplitude function \mathrm{am}(u,m) is the inverse function of F(\phi,m). That is given u we look for \phi such that u=F(\phi,m). In other words, we can write

(2)   \begin{equation*} u=\int_0^{\mathrm{am}(u,m)} \frac{d\theta}{\sqrt{1-m\sin^2\theta}}.\end{equation*}

These statements are false. For the correct definition of \mathrm{am}(u,m) for m><1 cf. The case of inverted modulus – Treading on Tiger’s tail.

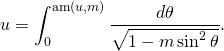
Now that the amplitude function is defined, we want to see it!
Wikipedia, the priceless source of all knowledge, provides one such view.

Clicking on the link there we are led to a monumental plaster model of the function, with the explanation that

Model in the collection of mathematical models and instruments, Georg-August-Universität Göttingen Göttingen. see also universitaetssammlungen.de/modelle for more information on the models

Another version of the same sculpture we can find ain the gallery of V. N. Karazin Kharkiv National University in Ukraine

However, there the fact that the model represents artistic cubism rather than realism is being noticed, though without discussion:

In most math software packages the Jacobi amplitude is a predefined special function. Below is an example in Mathematica (here m=k^2, and note that, unlike the plaster model, JacobiAmplitude[u,m] function in Mathematica is not symmetric w.r.t. the m=0 plane; see the source above)

Bravo! Better than Wikipedia, for sure. But not bravissimo. These plaster models, in Wikipedia and in Kharkiv University, are simply wrong.

Or maybe not? Sculpture is art and we are dealing with art here. For the Greeks and after, sculpture was supposed to represent reality. But at the beginning of the twentieth century this ambition has been renounced. New trends and movements have appeared with the aim of deforming the visible reality, sometimes but not always carrying some emotional charge. Picasso was at the frontiers of such a new direction – the cubism:

People were celebrating the unveiling of Picasso’s monumental sculpture in Chicago without being told neither its name nor its meaning. Another example is “Two Heads One Hand” by Mark Chagall (1964):

Here the shape to some extent resembles the reality it is supposed to represent, but only “to some extent”.

And the same is true about the plaster models of Jacobi elliptic amplitude function. The true shape, as rendered by Mathematica looks as follows:

This is clipped at the top and at the bottom, like in the plaster models. For m=0 we have \mathrm{am}(u,0)=u, because F(\phi,0)=\int_0^\phi d\theta=\phi. Therefore when we plot the amplitude function for u between -10 and 10 we need the vertical scale with the same range. The unclipped image is less impressive:

But there is no way we can get the symmetric plaster models featured in Wikipedia and Kharkiv University – they do not represent the mathematical reality, they belong to the world of cubism.

In the next post we will use the amplitude function to define two other elliptic functions that we will need for mathematical modeling of the Dzhanibekov effect – cn and dn.

P.S. This subject was to some extent first discussed in the comments to my Polish blog entry of October 10, 2016, “Euler rozszyfrowany” (Euler deciphered)

Update: Jan. 18, 2017
After the discussion under the post The case of inverted modulus – Treading on Tiger’s tail (thanks to BJAB) it appeared that to get the plaster model of \mathrm{am}(u,k^2) we need to include k>1. Here is the plot for <-4<k<4, 0<u<10.