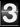Day: January 17, 2017

The case of inverted modulus – Treading on Tiger’s tail

Posted on by arkajad

According to I Ching, hexagram 10, when we are innocent, the tiger will not bite us even when we step on tiger’s tail.

There is a danger. Tigers are wild animals.

But, if we examine the signs carefully, there will be great good fortune.
A couple of days ago, when writing the post Jacobi Elliptic SN – The case of inverted modulus, and then writing Jacobi amplitude- realism or cubism, I stepped on tiger’s tail. Fortunately the tiger just looked at me with a forgiving smile and did not bite. I was lucky. Sure, I will have to correct the misleading pieces in those previous posts. But, thanks to good qcomments from BJAB, I have progressed with my understanding. The reading in Hexagram 10 includes:

The Judgement
Trading: Stepping on the tail of a tiger.
But it does not bite one. Success.
The Symbol
The heaven above and the lake below.
Symbolize Treading.
The superior man differentiates between high and low,
And thus fixes the minds of people.

Well, differentiating between high and low means making it clear how to define Jacobi elliptic functions for m>1 in terms of those with m<1. However, before fixing the mind of people I surely had to fix my own mind. This post is about how I did it …. till now. I must say that I was searching through all the available sources, and could not find a clear formulation. Perhaps it is one of those things that all experts know but do not bother to explain. Which would be however hard to understand, because in textbooks they often explain so many completely elementary issues…

Let us recall from Jacobi Elliptic SN – The case of inverted modulus:

The original name of Jacobi elliptic sn function was sinus amplitudinis. One contemplates the integral

(1)   \begin{equation*}u=\int_0^\phi\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}\end{equation*}

and calls \phi the amplitude \mathrm{am}(u,m) of u, where m=k^2. Then \mathrm{sn}(u,m) is defined as \sin\phi that is as \sin \mathrm{am}(u,m) – that is how sinus amplitudinis was invented.

First let us contemplate the integral 1. If |k|\leq 1, the integral is well defined (produces a finite number) for all finite values of \phi. The integrand is always positive, therefore u is strictly increasing function of \phi. The inverse function exists, \mathrm{am}(u,m) is well defined.

So far, so good, but then I continued with

But what if k>1? From the definition we see that u is antisymmetric function of \phi, therefore let us restrict ourselves to \phi nonnegative. If \phi is smaller that the critical value \phi_c defined by k^2\sin^2\phi_c=1, the integral is finite and is an increasing function of \phi. For \phi approaching \phi_c the integral becomes infinite. Therefore the inverse function \mathrm{am}(u,m) is well defined for all u, also for m>1.

And this was wrong. This was stepping on tiger’s tail. The sentence “For \phi approaching \phi_c the integral becomes infinite” is false. I wrote it because I thought it was true, but I did not care to verify. For m>1 the integral u remains finite for \phi=\phi_c.

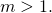
Nevertheless the rest of the derivation in that post is OK, as long as u is restricted to be the value of the integral. Therefore, for m>1, the formula

(2)   \begin{equation*} k\mathrm{sn}(u,m)=\mathrm{sn}(ku,1/m).\end{equation*}

holds, except that we have derived it for u such that

    \[|u|\leq \int_0^{\phi_c}\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}.\]

But nothing prevents us from defining \mathrm{sn}(u,m) as

(3)   \begin{equation*}\mathrm{sn}(u,m)=\frac{1}{k}\mathrm{sn}(ku,1/m)\end{equation*}

for m>1 and for all u. And this is what we do.

In order to be sure that this is what Wolfram’s Mathematica software “knows”, I checked:

I do not know which algorithm is being used by Mathematica for calculating sn function for m>1 (I suspect it is using complex Weierstrass functions), but evidently our definition above is correct (up to negligible numerical errors).

Once we are done with the sn function, we can now define the am function for m>1:

(4)   \begin{equation*}\mathrm{am}(u,m)=\arcsin(\mathrm{sn}(u,m)).\end{equation*}

We verify if this definition can be used for reproducing the plot of am in Jacobi amplitude- realism or cubism

And again we see that the definition above agrees with the one used by Mathematica – the difference between the two is zero. Our plot was correct. In fact, to be sure I asked to do the same plot by Maple. Here is the result:

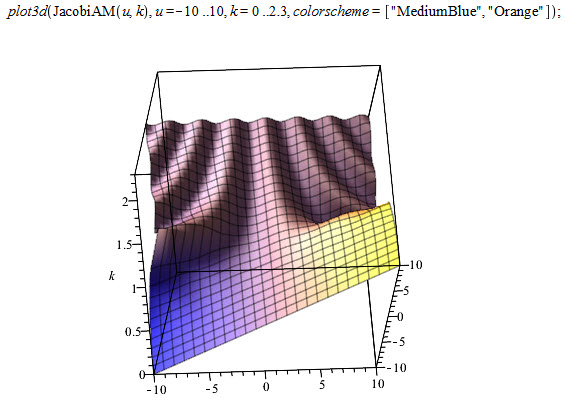
Maple is using the notation JacobiAM(u,k), where k^2=m.

Still good. Finally, what about Jacobi elliptic cosinus amplitudinis? Can we define it as \cos(\mathrm{am}(u,m)) also for m>1?
Again checking with Mathematica:

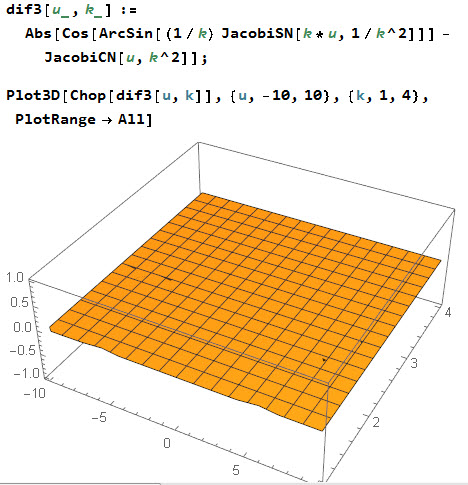
Good. Of course one can ask: since when Mathematica is a judge of what is a good definition of a mathematical function? It should not be so. But here we have to take into account the fact that mathematical monographs are surprisingly silent on the subject. It is like a conspiracy! Much like with UFO!

Now, I will have to fix the misleading parts in previous posts while hoping that I am on the right track now.