Day: January 21, 2017

Rescaled Jacobi amplitude – general solution for the mathematical pendulum

Posted on by arkajad

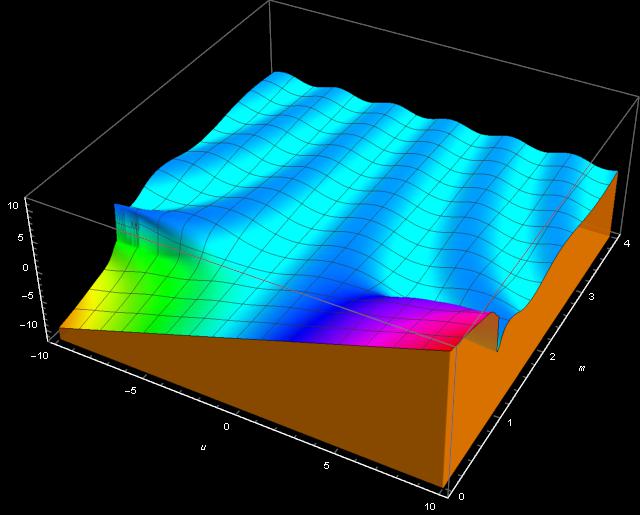
Jacobi amplitude function appeared yesterday in the episode Derivatives of Jacobi elliptic am, sn, cn, dn. We have derived a beautiful simple differential equation satisfied by this beautiful function


(1)   \begin{equation*}\left(\mathrm{am}'(u,m)\right)^2=1-m\,\sin^2(\mathrm{am}(u,m)),\quad \mathrm{am}(0,m)=0.\end{equation*}

Today we will see that, after rescaling, this is a perfect fabric for making the nonlinear outfit for the mathematical pendulum.
Wikipedia has smart animations showing pendulum’s motion for different kinetic energies, for instance

Initial angle of 45°

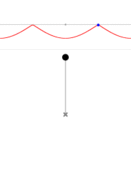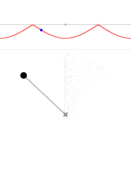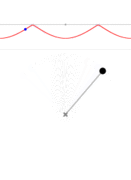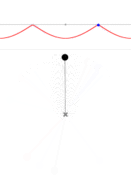
Pendulum with enough energy for a full swing.
It has also another little animation showing the angle \theta avrying with time.

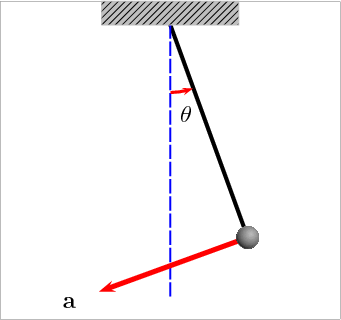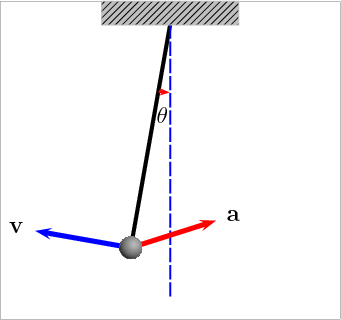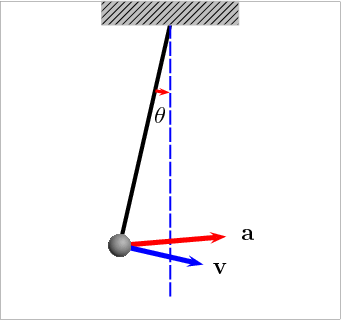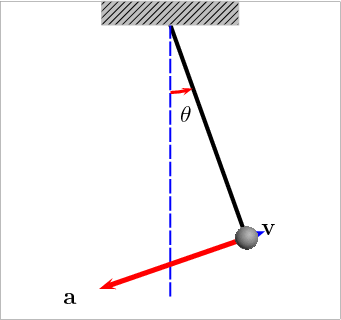
But this last picture is not well adapted for a pendulum that is making full swings around the circle. Therefore I will refer to the picture that I was already using in The case of the swinging pendulum:

This last picture has many more features depicted than I will need. I will need only the angles \theta and \theta/2 and the length of the pendulum l. The mass of the swinging point P I will denote by \mu. Usually it is denoted by m, but we will use m for the square of the modulus m=k^2 of the Jacobi amplitude function \mathrm{am}(u,m).

For solving our pendulum problem we will only need conservation of energy.

When the pendulum swings, the angle \theta(t) changes with time t. We will use the dot to denote time derivative of \theta

    \[\dot{\theta}=d\theta(t)/dt.\]

The linear velocity V of the pendulum is V=l\dot{\theta}, therefore the kinetic energy E_k is

    \[E_k=\frac{\mu V^2}{2}=\frac{\mu l^2\dot{\theta}^2}{2}.\]

For the potential energy we will choose the zero of the potential at the bottom, Denoting by h the height of the mass with respect to the lowest level, we have

    \[ h= l(1-\cos\theta).\]

For \theta=0 we have h=0, for \theta=\pi we have h=2l. Here it is useful to introduce the half-angle \phi=\theta/2. We know from trigonometry that

    \[ 1-\cos \theta =2 \sin^2 \theta/2.\]

Therefore

(2)   \begin{equation*} h = 2l\sin^2 \phi.\end{equation*}

Potential energy E_p is \mu g h, that is

(3)   \begin{equation*}E_p=2\mu gl \sin^2\phi.\end{equation*}

Maximum kinetic energy E_{k,max} is at the bottom, for \theta=0. At this point we have also minimum potential energy, since E_p=0 at the point. Maximal potential energy E_{p,max} is at the top: E_{p,max}=2\mu g l.

The character of the motion will depend on the ratio E_{p,max}/E_{k,max}. When this ratio is >1, there will be not enough kinetic energy to rise the swinging mass to the top, and the pendulum will oscillate back and forth. But when the ratio E_{p,max}/E_{k,max}<1, then
even at the top the mass will have a nonzero speed, and the pendulum will be making full circles. We denote this important ratio by m

    \[ m=k^2\stackrel{df}{=}\frac{E_{p,max}}{E_{k,max}}.\]

Thus

(4)   \begin{equation*} E_{k,max}=\frac{2\mu gl}{m}.\end{equation*}

We now write the conservation of energy equation:

    \[ E_k+E_p=E_{k,max}.\]

On the left we have total energy at time t. On the right we have total energy at the bottom, when there is only kinetic energy. Substituting the E_k,E_p,E_{k,max} with the corresponding expressions derived above we get

(5)   \begin{equation*} \frac{1}{2}\mu l^2 \dot{\theta}^2+2\mu gl \sin^2\phi=\frac{2\mu gl}{m}.\end{equation*}

Now, \theta=2\phi, therefore \dot{\theta}^2=4\dot{\phi}^2.
We also introduce \omega defined as

(6)   \begin{equation*}\omega=\sqrt{\frac{g}{l}}.\end{equation*}

This is the expression for the standard angular frequency for a linear pendulum, fo small oscillations.

With all these substitutions and simplifications Eq. (5) can be written in the following form:

(7)   \begin{equation*}\frac{m}{\omega^2}\dot{\phi}^2=1-m\,\sin^2\phi.\end{equation*}

The last equation is almost identical with the equation (1) satisfied by the amplitude function, except for the coefficient \frac{m}{\omega^2} in front of \dot{\phi}^2 on the left. But this can be easily accomodated by changing the time scale. With m=k^2 we notice that

    \[\frac{k^2}{\omega^2}\left(\frac{d}{dt}\,\mathrm{am}(\frac{\omega t}{k},m)\right)^2=\left(\mathrm{am}'(\frac{\omega t}{k},m)\right)^2=1-m\,\sin^2(\mathrm{am}(\frac{\omega t}{k},m)).\]

Comparing with Eq. (7) we see that the solution of the pendulum equation is

(8)   \begin{equation*}\phi(t)=\mathrm{am}(\frac{\omega t}{k},m),\end{equation*}

and therefore

(9)   \begin{equation*}\theta(t) = 2\,\mathrm{am}(\frac{\omega t}{k},m)\end{equation*}

.

In the next post we will look closer at this solution and try to understand its meaning.