According to Wikipedia special relativity theory was originally proposed in 1905 by Albert Einstein. But Wikipedia is not always the best source of information. For instance Wikipedia has a section about “Causality and prohibition of motion faster than light“. Quite often we can read sentences like that one:
” Since the moving clouds travel slightly slower than the speed of light, they do not actually violate Einstein’s theory of relativity which sets light as the speed limit.”
while elsewhere you can read:
It continues to be alleged that superluminal influences of any sort would be inconsistent with special relativity for the following three reasons: (i) they would imply the existence of a ‘distinguished’ frame; (ii) they would allow the detection of absolute motion; and (iii) they would violate the relativity of simultaneity. This paper shows that the first two objections rest upon very elementary misunderstandings of Minkowski geometry and lingering Newtonian intuitions about instantaneity. The third objection has a basis, but rather than invalidating the notion of faster-than-light influences it points the way to more general conceptions of simultaneity that could allow for quantum nonlocality in a natural way.
The point is that very often physicists do not think. They repeat what someone told them, or what they read, without much thinking. To quote from “Superluminal motions?A bird-eye view of the experimental situation“, Found.Phys.31:1119-1135,2001, by Erasmo Recami
… Still in pre-relativistic times, one meets various related works, from those by J.J.Thomson to the papers by the great A.Sommerfeld. With Special Relativity, however, since 1905 the conviction spread over that the speed c of light in vacuum was the upper limit of any possible speed. For instance, R.C.Tolman in 1917 believed to have shown by his “paradox” that the existence of particles endowed with speeds larger than c would have allowed sending information into the past. Such a conviction blocked for more than half a century (aside from an isolated paper (1922) by the Italian mathematician G.Somigliana) any research about Superluminal speeds.
Science is not free from “religious wars”. But that is not the subject of my post today. My post is about a certain curious observation that gave me some idea, and I do not know whether this idea is new, or it already occurred to someone else before. And I do not care, because the idea may be not crazy enough to be worth of discussing. Nevertheless it fits the subject of discussion in my recent series, so I will tell it to you now, and, perhaps, ask some questions.
In Special relativity we have a strange formula for addition of velocities (here we will discuss only velocities in one space dimension):

Q & A: Relativistic velocity addition

To simplify the notation I will assume that ![]() or, if you wish, I will understand my velocity
or, if you wish, I will understand my velocity ![]() as the quotient
as the quotient ![]() etc.
etc.
The relativistic addition of velocities is sometimes denoted as ![]()
(1) ![]()
John Baez, whom we know from my previous posts, has a web page on How Do You Add Velocities in Special Relativity? There he notices the well know fact that the relativistic addition of velocities is essentially the same as for hyperbolic tangent, where we have
(2) ![]()
One of the consequences of the above addition formula is that if, say ![]() and
and ![]() then
then ![]()
Your spaceship moves with respect to the Sun with velocity that of 90% of the speed of light, and you send from it, in the direction of its flight, a missile traveling with respect to the spaceship with another 90% speed of light, and yet, with respect to the Sun the missile has the speed of 99% of the speed of light, rather than 180% as we would expect from naive addition.
Now, in the recent series of posts we were discussing elliptic functions, and in particular Jacobi sinus function ![]() We know that for the parameter
We know that for the parameter ![]() we have
we have ![]() We also have addition formula for
We also have addition formula for ![]() . It is thus natural to ask how would special relativity look like when the formula (1) is replaced by one derived from the addition formula for
. It is thus natural to ask how would special relativity look like when the formula (1) is replaced by one derived from the addition formula for ![]() given in the post Elliptic addition theorem:
given in the post Elliptic addition theorem:
(3) ![]()
We can set ![]() then
then ![]()
![]() and the new, proposed addition formula, involving parameter
and the new, proposed addition formula, involving parameter ![]() not ncessrily equal to 1, reads:
not ncessrily equal to 1, reads:
(4) ![]()
That is my candidate for the m-deformed relativity. How it compares with the non-deformed (that is “standard”) relativity? It looks weird.
Assume our space-ship travels with the speed 90% of the speed of light. Assume ![]() , and assume we shoot a missile from our ship, in the direction of its motion. What will be the speed of the missile? Here are the plots:
, and assume we shoot a missile from our ship, in the direction of its motion. What will be the speed of the missile? Here are the plots:

The blue curve is the special relativity. The ![]() speed always increases, though slower and slower as
speed always increases, though slower and slower as ![]() approaches 1. But the m-deformed relativity, represented by the red curve is even crazier. If the missile is shot with a speed over a certain value, it starts to move slower with respect to the Sun.
approaches 1. But the m-deformed relativity, represented by the red curve is even crazier. If the missile is shot with a speed over a certain value, it starts to move slower with respect to the Sun.
Is that crazy enough to have a chance to be useful?
Can these elliptically deformed addition formulas be included in some geometrical setting? Will it follow from some algebra involving a generalization of the Lorentz group? I do not know.




How does formula (3) look like for m=1 ?
For we have
we have
 and
and 
Therefore we have
or
and you get the standard formula for
Thanks for corrections!
Is it a group for m<1 (m not equal 1) (associativity)?
What is the maximum value of red curve?
We know that sn(4K,m)=1. So the max is always 1.
Associativity follows from sn((u+v)+t)=sn(u+(v+t))
sn(4K,m)=1 ?
I thought that zero.
Sorry, my mistake. Should be sn(K,m)=1.
How much is K(0.9)?
Ark,
well, I used wolframalpha.
They say that
sn((K(0.9)-sn^(-1)(0.9|0.9))|0.9)
equals to
0.8373213308342925…
and this is rather coherent with your red curve.
What do you think of it?
(I had a little headache with all that zero-point-nines.)
K(0.9)=2.57809
We have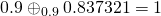
My comment 2017/01/31 at 15:28
Your comment 2017/01/31 at 15:27
We are synchronised somehow.
Entanglement perhaps.
Heh, aż mi się paszcza prawie dookoła głowy uśmiechnęła :) Bardzo to fajne. Ciekawe czy to tylko matematyczna sztuczka, czy może coś więcej…
Pozdrowienia dla Pana i Bjaba