Last few days I was busy trying to understand some subtle points about Jacobi elliptic functions that I could not find clearly explained neither in Wikipedia nor in the literature that I was searching in the libraries and on internet. On internet I was able to find old treaties by the classics, like Legendre, as well as other old textbooks at archive.org. But nowhere I was able to find a clear explanation of how one can define in a simple way Jacobi elliptic functions am, sn, cn, dn for modulus k greater than 1. Finally, with the help stemming from useful comments, everything seems to fall in place.

In fact yesterday I wrote to prof. William A. Schwalm asking for some suggestions. He kindly wrote me back suggesting reading Chapter 4.3 of his monograph Lectures on Selected Topics in Mathematical Physics: Elliptic Functions and Elliptic Integrals (IOP Concise Physics) May 31, 2016. I did not have this book, so I bought it – the Kindle edition, instatly delivered to my Kindle. And yet, after perusing I could find what I was looking for. Will try to study deeper.
In the previous post, owing to the discussion with BJAB, I was able to create a graph that is a replica of the plaster model of Jacobi’s amplitude function that I have discussed and criticized in Jacobi amplitude- realism or cubism. I fixed that post – with an addendum at the bottom.

I was wrong. Now all becomes clear. So I wrote email to the mathematicians in Kharkiv that are in charge of the web page on Jacobi amplitude. I have send them my Mathematica notebook that reproduces the plaster model – which they were not able to reproduce with their Mathematica code.
So, with some meandering, there is some progress. Let us continue.
In the previous post, The case of inverted modulus – Treading on Tiger’s tail, We have defined Jacobi’s sinus amplitudinis ![]() for all real
for all real ![]() and all real
and all real ![]() We have defined it as
We have defined it as ![]() For
For ![]() we have defined
we have defined ![]() and
and ![]() as
as
(1) ![]()
(2) ![]()
We have then defined cosinus amplitudinis for ![]() as
as
(3) ![]()
It follows from these definitions that
(4) ![]()
for all real ![]() and
and ![]()
While elliptic sn and cn functions may be considered as “deformations” of circular trigonometric functions sinus and cosinus, there is also the third function dn(u,m) that can be considered as a deformation of the constant function 1. For ![]() it is defined as
it is defined as
(5) ![]()
For ![]() we have
we have ![]() while for
while for ![]() from Eqs (4) and (5), we have
from Eqs (4) and (5), we have
![]()
From Eq. (2), for ![]() we have that
we have that ![]() Therefore, for
Therefore, for ![]() we have that
we have that ![]() Therefore
Therefore
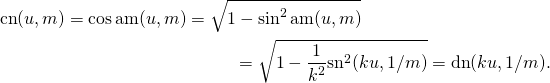
Thus
(6) ![]()
Setting ![]()
![]() we can now extend the above property for defining
we can now extend the above property for defining ![]() for
for ![]() :
:
(7) ![]()
Notice that while for ![]() the function
the function ![]() is nonnegative, for
is nonnegative, for ![]() it is oscillating between positive and negative values. Nevertheless the following relations hold true also for
it is oscillating between positive and negative values. Nevertheless the following relations hold true also for ![]()
(8) ![]()
Indeed, assuming ![]() from Eq. (1) and Eq. (4) we have
from Eq. (1) and Eq. (4) we have
![]()



The plaster model and graphs for k which varies from positives to negatives seems artificial to me.
I don’t see why k should be considered negative.
On contrary u could be not only positive but also negative for the model and graph.
k varies from negative to positive for symmetry, superfluous, but it is artistic effect.
u could be negative, but we skip the negative part to save the artist’s work and the plaster, and to achieve the a specific visual experience.
Thanks for the erratum. Fixed.
Another thing is that when we consider not only m1 we should not name functions as elliptic but as ellipso-hyperbolic (due to hyperbolic geometric definiton).