Elliptic Pi in Mathematica and Maple

Posted on by arkajad

We use EllipticPi when we write exact solutions of rotation of a free asymmetric top. While solving Euler’s equations for angular velocity or angular momentum in the body frame we need Jacobi elliptic functions \cn,\sn,\dn, solving the differential equation for the attitude matrix involves EllipticPi function. As I have explained it in Taming the T-handle continued we need the integral

(1)   \begin{equation*}\psi(t)=c_1 t+c_2\int_0^t \frac{1}{1+c_3\,\sn^2(Bs,m)}\,ds.\end{equation*}

In Mathematica this is easily implemented as

(2)   \begin{equation*}\psi(t)=c_1 t+\frac{c_2}{B}\,\Pi(-c_3;\am(Bt,m)|m).\end{equation*}

However, as pointed out by Rowan in a comment to Taming the T-handle continued , the same formula does not work with Maple.

While the documentations of both Mathematica and Maple contain links to Abramowitz and Stegun Handbook of Mathematical Functions, they use different definitions. Here is what concerns us, from p. 590 of the 10th printing:

What we need is 17.2.16, while Maple is using 17.2.14. To convert we need to set x=\sn u, but such a conversion is possible only in the domain where \sn can be inverted. We can do it easily for sufficiently small values of u, but not necessarily for values that contain several quarter-periods.

The following Maple procedure does the job:


epi := proc (t::float, nu::float, k::float) local t2, n, dt, ep0, res; ep0 := EllipticPi(nu, k); t2 := EllipticK(k); n := floor(t/t2); dt := t-t2*n; if type(n, even) then res := Re(n*ep0+EllipticPi(JacobiSN(dt, k), nu, k)) else res := Re((1+n)*ep0-EllipticPi(JacobiSN(t2-dt, k), nu, k)) end if end proc

HAs an example here is the Maple plot for nu=-3, k=0.9:
plot(('epi')(t, -3.0, .9), t = -20 .. 20)

And here is the corresponding Mathematica plot:

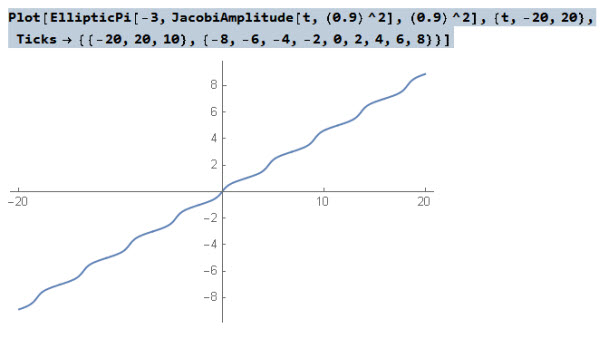
The function epi(t,nu, k) defined above for Maple gives now the same result as EllipticPi(nu,JacobiAM(t,k^2),k^2) in Mathematica.

19 thoughts on “Elliptic Pi in Mathematica and Maple”

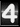
  1. Thank you. I tried posting last night but never appeared.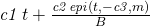
    this is what I am entering into the function {\it c1}\,t+{\frac {{\it c2}\,{\it epi} \left( t,-{\it c3},m \right) }{B}}
    This not sure whether the sign of c3 is correct, I based it on your numerical example and whether I should use m or squart root of m. Handbook of Mathematical Functions arrived today. Will see if I can get a clearer insight from that over the next while too.

  2. I was messing up with the blog, trying another comments method.

    I think you need Bt and not t as an rgument. And you need k, not m. But I will check and let you know…

  3. Just trying to clear up some of my earlier confusions.

    In an earlier reply when you said “Maple is using the modulus m as the second argument of am,sn,cn,dn. I am using m=k^2 as the second argument (like in Matlab and in Mathematica).” because I was saying I got squareroot of your value for m. So I should really name it “k”. Maple gives defn.
    {\it JacobiSN} \left( z,k \right) =\sin \left( {\it JacobiAM} \left( z ,k \right) \right)
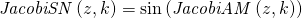
    That clears up one source of confusion if I am correct.

  4. In the post “Taming the T-handle continued”, and also above, B was missing in the argument of the amplitude function. Now I have it corrected. Here is Maple code that gives correct value of psi:

    Please, notice that Maple puts nu as the second argument. I have respected this order in the definition of epi. So Bt enters as the first argument.

  5. Thank you Ark,
    Hopefully one of these links to my animation works,
    [IMG]http://i67.tinypic.com/29ncda1.jpg[/IMG]
    or this
    http://tinypic.com/m/jsbzq1/2

    http://tinypic.com/usermedia.php?uo=bpRy0IYlPgOg2exx4%2Fn43Ih4l5k2TGxc#.WK-R-sJ-haQ

    I haven’t use theses sort of links before so need to learn about that to.

    I am not really to happy with my product. It is jumpy but if I wait for perfection I will never show anything. There are jerks in the motion that make it look like it bouncing of something.

  6. I would be happy to share the code. How did you get the “epi” procedure from Maple and post it. Because I just copied and pasted it in. Most exports from Maple are unreadable. I could try export whole document as latex and see what happens. I work in document mode will try worksheet mode. Will take experimenting. Will tidy it up a bit too and add annotations.

  7. Ctrl-C Ctrl-V it is. Though it has taken out all the comments. The code may not be efficient. It’s just the way it figured it out with help on MaplePrimes forum to get animations to display.

    restart;

    with(plots);

    with(plottools);
    OriginalBody := display([point([1, -.2, 0], colour = red, symbolsize = 50, symbol = solidsphere), point([-1, -.2, 0], colour = red, symbolsize = 50, symbol = solidsphere), point([0, 1, 0], colour = purple, symbolsize = 50, symbol = solidsphere), line([0, 0, 0], [1, -.2, 0]), line([0, 0, 0], [-1, -.2, 0]), line([0, 0, 0], [0, 1, 0]), line([0, 0, 0], [.5, 0, 0], colour = red, thickness = 4), line([0, 0, 0], [0, .5, 0], colour = yellow, thickness = 4), line([0, 0, 0], [0, 0, .5], colour = blue, thickness = 4)], scaling = constrained);

    epi := proc (t, nu, k) local t2, n, dt, ep0, res; ep0 := EllipticPi(nu, k); t2 := EllipticK(k); n := floor(t/t2); dt := t-t2*n; if type(n, even) then res := Re(n*ep0+EllipticPi(JacobiSN(dt, k), nu, k)) else res := Re((1+n)*ep0-EllipticPi(JacobiSN(t2-dt, k), nu, k)) end if end proc;
    NULL;
    I1 := 1; I2 := 2; I3 := 3; d := (1/1000)*(499+0); L := 1;
    c1 := 1/I3;
    c2 := 1/I1-1/I3;
    c3 := I3*(I2-I1)/(I1*(I3-I2));

    A1 := L*sqrt(I1*(I3*d-1)/(I3-I1));
    A2 := L*sqrt(I2*(I3*d-1)/(I3-I2));
    A3 := L*sqrt(I3*(-I1*d+1)/(I3-I1));
    B := L*sqrt(I3-I2)*sqrt(-I1*d+1)/(sqrt(I1)*sqrt(I2)*sqrt(I3)); m := (I3*d-1)*(I2-I1)/((I3-I2)*(-I1*d+1));
    “(->)”
    k := sqrt(m);
    “(->)”
    L1 := A1*JacobiCN(B*t, k);
    L2 := A2*JacobiSN(B*t, k);
    L3 := A3*JacobiDN(B*t, k);
    Lp := sqrt(L1^2+L2^2);
    if d )”
    “(->)”
    NULL;
    psi := simplify(expand(expand(psi)), assume = real);
    NULL;
    Q1 := evalf(Matrix(3, 3, [[cos(psi), -sin(psi), 0], [sin(psi), cos(psi), 0], [0, 0, 1]]));

    Q0 := Matrix(3, 3, [[L1*L3/(L*Lp), L2*L3/(L*Lp), -Lp/L], [-L2/Lp, L1/Lp, 0], [L1/L, L2/L, L3/L]]);

    Q := simplify(Q1 . Q0, size);
    components := evalf(Q^%T . Vector(3, [0, 0, L]));

    NULL
    c1 := Vector(3, [1, -.2, 0]);
    c2 := Vector(3, [-1, -.2, 0]);
    c3 := Vector(3, [0, 1, 0]);
    c4 := Vector(3, [1, -.2, 0]);
    c5 := Vector(3, [-1, -.2, 0]);
    c6 := Vector(3, [0, 1, 0]);
    c7 := Vector(3, [.35, 0, 0]);
    c8 := Vector(3, [0, .35, 0]);
    c9 := Vector(3, [0, 0, .35]);
    c10 := Vector(3, [components[1], 0, 0]);
    c11 := Vector(3, [0, components[2], 0]);
    c12 := Vector(3, [0, 0, components[3]]);
    c := [seq(c || n, n = 1 .. 12)];

    Trnsc := evalf(seq(Q . c[n], n = 1 .. 12));
    NULL
    t1 := 13; t2 := 52; frm := 100;
    plot(psi, t = t1 .. t2);
    NULL
    Bdyprt1 := unapply(display(POINTS([Trnsc[1][1], Trnsc[1][2], Trnsc[1][3]]), colour = red, symbolsize = 50, symbol = solidsphere), t); Bdyprt1a := plots:-animate(Bdyprt1, [t], t = t1 .. t2, frames = frm);
    Bdyprt2 := unapply(display(POINTS([Trnsc[2][1], Trnsc[2][2], Trnsc[2][3]]), colour = red, symbolsize = 50, symbol = solidsphere), t); Bdyprt2a := plots:-animate(Bdyprt2, [t], t = t1 .. t2, frames = frm);
    Bdyprt3 := unapply(display(POINTS([Trnsc[3][1], Trnsc[3][2], Trnsc[3][3]]), colour = purple, symbolsize = 50, symbol = solidsphere), t); Bdyprt3a := plots:-animate(Bdyprt3, [t], t = t1 .. t2, frames = frm);
    Bdyprt4 := unapply(display(line([0, 0, 0], [Trnsc[4][1], Trnsc[4][2], Trnsc[4][3]])), t); Bdyprt4a := plots:-animate(Bdyprt4, [t], t = t1 .. t2, frames = frm);

    Bdyprt5 := unapply(display(line([0, 0, 0], [Trnsc[5][1], Trnsc[5][2], Trnsc[5][3]])), t); Bdyprt5a := plots:-animate(Bdyprt5, [t], t = t1 .. t2, frames = frm);
    Bdyprt6 := unapply(display(line([0, 0, 0], [Trnsc[6][1], Trnsc[6][2], Trnsc[6][3]])), t); Bdyprt6a := plots:-animate(Bdyprt6, [t], t = t1 .. t2, frames = frm);
    Bdyprt7 := unapply(display(line([0, 0, 0], [Trnsc[7][1], Trnsc[7][2], Trnsc[7][3]], colour = red, thickness = 1)), t); Bdyprt7a := plots:-animate(Bdyprt7, [t], t = t1 .. t2, frames = frm); arx := unapply((‘display’)((‘plots:-arrow’)([0, 0, 0], [Trnsc[10][1], Trnsc[10][2], Trnsc[10][3]], width = 0.2e-1, shape = cylindrical_arrow, colour = red)), t); arxa := (‘animate’)(‘arx’, [t], t = t1 .. t2, frames = frm); Vcx := unapply(display(line([0, 0, 1], [Trnsc[10][1], Trnsc[10][2], Trnsc[10][3]], colour = red, thickness = 1, linestyle = dash)), t); Vcxa := plots:-animate(Vcx, [t], t = t1 .. t2, frames = frm); tx := unapply((‘display’)((‘plots:-textplot3d’)([Trnsc[7][1], Trnsc[7][2], Trnsc[7][3], “X”])), t); txa := (‘animate’)(‘tx’, [t], t = t1 .. t2, frames = frm);
    Bdyprt8 := unapply(display(line([0, 0, 0], [Trnsc[8][1], Trnsc[8][2], Trnsc[8][3]], colour = “GreenYellow”, thickness = 1)), t); Bdyprt8a := plots:-animate(Bdyprt8, [t], t = t1 .. t2, frames = frm); ary := unapply((‘display’)((‘plots:-arrow’)([0, 0, 0], [Trnsc[11][1], Trnsc[11][2], Trnsc[11][3]], width = 0.2e-1, shape = cylindrical_arrow, colour = “GreenYellow”)), t); arya := (‘animate’)(‘ary’, [t], t = t1 .. t2, frames = frm); Vcy := unapply(display(line([0, 0, 1], [Trnsc[11][1], Trnsc[11][2], Trnsc[11][3]], colour = “GreenYellow”, thickness = 1, linestyle = dash)), t); Vcya := plots:-animate(Vcy, [t], t = t1 .. t2, frames = frm); ty := unapply((‘display’)((‘plots:-textplot3d’)([Trnsc[8][1], Trnsc[8][2], Trnsc[8][3], “Y”])), t); tya := (‘animate’)(‘ty’, [t], t = t1 .. t2, frames = frm);
    Bdyprt9 := unapply(display(line([0, 0, 0], [Trnsc[9][1], Trnsc[9][2], Trnsc[9][3]], colour = blue, thickness = 1)), t); Bdyprt9a := plots:-animate(Bdyprt9, [t], t = t1 .. t2, frames = frm); arz := unapply((‘display’)((‘plots:-arrow’)([0, 0, 0], [Trnsc[12][1], Trnsc[12][2], Trnsc[12][3]], width = 0.2e-1, shape = cylindrical_arrow, colour = blue)), t); arza := (‘animate’)(‘arz’, [t], t = t1 .. t2, frames = frm); Vcz := unapply(display(line([0, 0, 1], [Trnsc[12][1], Trnsc[12][2], Trnsc[12][3]], colour = blue, thickness = 1, linestyle = dash)), t); Vcza := plots:-animate(Vcz, [t], t = t1 .. t2, frames = frm); tz := unapply((‘display’)((‘plots:-textplot3d’)([Trnsc[9][1], Trnsc[9][2], Trnsc[9][3], “Z”])), t); tza := (‘animate’)(‘tz’, [t], t = t1 .. t2, frames = frm);
    ar1 := plots:-arrow([0, 0, 0], [0, 0, L], width = 0.2e-1, shape = cylindrical_arrow, colour = black);
    display(ar1, arxa, arya, arza, txa, tya, tza, Vcxa, Vcya, Vcza, Bdyprt1a, Bdyprt2a, Bdyprt3a, Bdyprt4a, Bdyprt5a, Bdyprt6a, Bdyprt7a, Bdyprt8a, Bdyprt9a, scaling = constrained, labels = [x, y, z], title = “=d”*d);

    NULL;

  10. if d “less than” 1/2 then psi := c1*t+c2*epi(B*t, -c3, k)/B else psi := L*t/I2+L*arctan(t*sqrt(I3*(I2-I1)/(I1*(I3-I2)))*tanh(sqrt((I2-I1)*(I3-I2)/(I1*I2^2*I3)))) end if

    “less than” change this to the less than symbol. The less than symbol blanks out the rest of the line when I copied and pasted here.

    Ignore “(->)” and NULL;

  14. Oh. I have made a major error. I didn’t include the case of d>1/2.
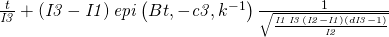
    I have psi as
    {\frac {t}{{\it I3}}}+{ \left( {\it I3}-{\it I1} \right) {\it epi} \left( Bt,-{\it c3},{k}^{-1} \right) {\frac {1}{\sqrt {{\frac {{\it I1}\,{\it I3}\, \left( {\it I2}-{\it I1} \right) \left( d{\it I3}-1 \right) }{{\it I2}}}}}}}
    using the epi function you gave me. I dont think I have the correct values entered into epi.

Leave a Reply