Standing on the shoulders of giants may be good, even very-very good. But at the same time it can be very dangerous. First of all it is a dangerous balancing act. It is easy to fall.

But what if the giant gets a hiccup? Or stumble? You may die. Or someone can die because of aftershocks.
In Standing on the shoulders of giants I quoted two papers that I used in working out my computer simulations of Dzhanibekov’s effect. These were
Ramses van Zon, Jeremy Schofield, “Numerical implementation of the exact dynamics of free rigid bodies“, J. Comput. Phys. 225, 145-164 (2007)
and
Celledoni, Elena; Zanna, Antonella.E Celledoni, F Fassò, N Säfström, A Zanna, The exact computation of the free rigid body motion and its use in splitting methods, SIAM Journal on Scientific Computing 30 (4), 2084-2112 (2008)
The algorithms were working smoothly. But recently I decided to use quaternions instead of rotation matrices. And in recent post Introducing geodesics, I have presented a little animation:
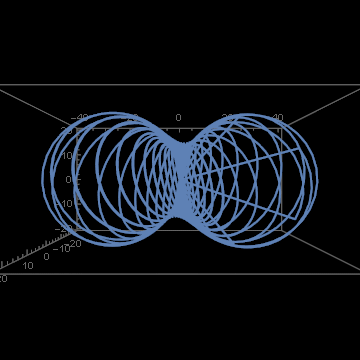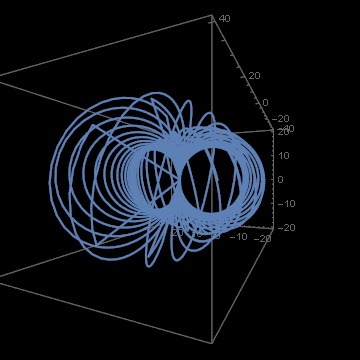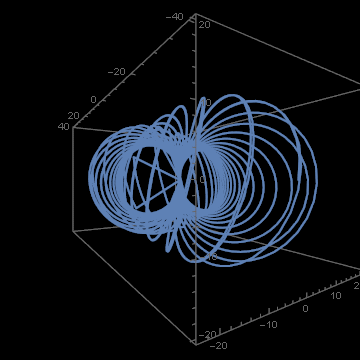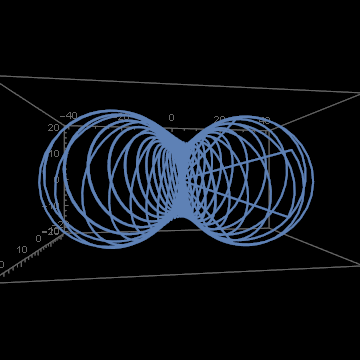
It looks impressive, but if we pay attention to details, we see something strange:

We have a nice curly trajectory, but there are also strange straight line spikes. On animation they are, perhaps, harmless. But if something like this happens with the software controlling the flight of airplanes, space rockets or satellites – people may die. There is a BUG in the algorithm. Yes, I did stay on shoulders of giants, but perhaps they were not the right giants for my aims? And indeed this happens. The method I used is not appropriate for working with quaternions.
That is why I have to do the reboot, and look for another giant. Here is my giant:
 Antonella Zanna, professor of Mathematics, University of Bergen, specialty Numerical Analysis/Geometric Integration.
Antonella Zanna, professor of Mathematics, University of Bergen, specialty Numerical Analysis/Geometric Integration.
I am going to use the following paper:
Elena Celledoni, Antonella Zanna, et al. “Algorithm 903: FRB–Fortran routines for the exact computation of free rigid body motions.” ACM Transactions on Mathematical Software, Volume 37 Issue 2, April 2010, Article No. 23, doi:10.1145/1731022.1731033.
The paper is only seven years old. And it has all what we need. As in Standing on the shoulders of giants we will split the attitude matrix ![]() into a product:
into a product: ![]() but this time we will do it somewhat smarter. Celledoni and Zanna denote the angular momentum vector in the body frame using letter
but this time we will do it somewhat smarter. Celledoni and Zanna denote the angular momentum vector in the body frame using letter ![]() and they assume that
and they assume that ![]() is normalized:
is normalized: ![]() They assume, as we do,
They assume, as we do, ![]() and use
and use ![]() to denote the kinetic energy. Let us first look at the following part of their paper (which is available here):
to denote the kinetic energy. Let us first look at the following part of their paper (which is available here):

Though it is not very important, I must say that it is very nice of the two authors that they acknowledge Kosenko. I was trying to study Kosenko’s paper, but I gave up not being able to understand it. Then wen notice that the case considered is that of ![]() using the notation in my posts. That means “high energy regime”.
using the notation in my posts. That means “high energy regime”.
The angular momentum ![]() is constant (fixed) in the laboratory frame owing to the conservation of angular momentum. Suppose we orient the laboratory frame so that its z axis is oriented along the angular momentum vector. Then, in the laboratory frame angular momentum has coordinates
is constant (fixed) in the laboratory frame owing to the conservation of angular momentum. Suppose we orient the laboratory frame so that its z axis is oriented along the angular momentum vector. Then, in the laboratory frame angular momentum has coordinates ![]() Suppose we construct a matrix
Suppose we construct a matrix ![]() that transforms
that transforms ![]() into
into ![]() . The attitude matrix
. The attitude matrix ![]() transforms vector components in the body frame into their components in the laboratory frame. In particular it transforms
transforms vector components in the body frame into their components in the laboratory frame. In particular it transforms ![]() into
into ![]() . Therefore,if we write
. Therefore,if we write ![]() the matrix
the matrix ![]() must transform
must transform ![]() into itself. Therefore
into itself. Therefore ![]() must be a rotation about the third axis, that is it is of the form:
must be a rotation about the third axis, that is it is of the form:
(1) 
All of that we have discussed already in Standing on the shoulders of giants. But now we are going to choose ![]() differently.
differently.
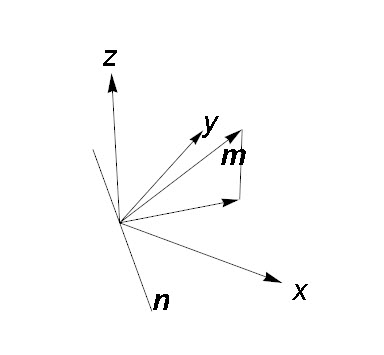
So suppose we have vector ![]() of unit length. What would be the most natural way of constructing a rotation matrix that rotates
of unit length. What would be the most natural way of constructing a rotation matrix that rotates ![]() into
into ![]() ? Simple. Project
? Simple. Project ![]() vertically onto
vertically onto ![]() plane. Draw a line
plane. Draw a line ![]() on
on ![]() plane that is perpendicular to the projection. Rotate about this line by the angle
plane that is perpendicular to the projection. Rotate about this line by the angle ![]() between
between ![]() and
and ![]()
Let us now do the calculations. Vector ![]() has components
has components ![]() Its projection on
Its projection on ![]() plane has components
plane has components ![]() Orthogonal vector in
Orthogonal vector in ![]() plane has components
plane has components ![]() (to check orthogonality calculate scalar product), So the normalized vector
(to check orthogonality calculate scalar product), So the normalized vector ![]() has components
has components
![]()
where
![]()
The cosinus of the angle ![]() is
is ![]() Its sinus is
Its sinus is ![]()
In Spin – we know that we do not know we have derived a general formula for a rotation about an angle ![]() about axis defined by a unit vector
about axis defined by a unit vector ![]() :
:
![]()
where for any vector ![]()
(2) 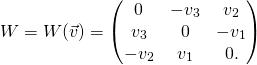
Applying the formula to our case, simple algebra leads to:
(3) 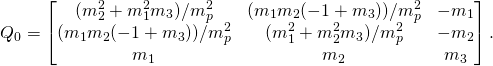
We can easily check that indeed ![]() is an orthogonal matrix with determinant 1,
is an orthogonal matrix with determinant 1, ![]() acting on
acting on ![]() vector gives
vector gives ![]() One can also check that the vector
One can also check that the vector ![]() is invariant under
is invariant under ![]() – as it should be as it is on the rotation axis. REDUCE program that checks it all is here.
– as it should be as it is on the rotation axis. REDUCE program that checks it all is here.
At this point we have to make a break. It is not yet clear what is the relation of my ![]() to the paper quoted, what is the difference between this and the old version, and why is this version better?
to the paper quoted, what is the difference between this and the old version, and why is this version better?
We will continue climbing on the shoulders of giants in the following notes. But, please, remember, Standing on shoulders of giants (like “Nobel Prize Winner” Obama), is risky:





Ark,
today the World delivered me the thought:
“Did you finish with your sequence?”
Under your post Never twice the same
I asked:
“
Where is the limit of this sequence?”
Now the sequence looks like:
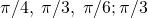
But is it finished?
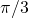 or
or 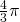 ?
?
From symmetry there should be fifth term:
Do you agree?
Have to think about it. Today I have first to understand what the giants say. Could not sleep.
Why don’t YOU finish the sequence while I am busy with the giants?
Take a break from the giants.
I gave the proposition of the fifth term.
A bug in your post “Never twice the same” is deeply hidden and I couldn’t find it so far.
OK. Will take a break. Fortunately I was able to reproduce one numerical result from the giants code.
And thanks for multi-errata.
“Applying the formula to our case, simple algebra leads to:”
I applied formulas to our case and I got something wich is not as your but
but 
So maybe we should take not Rodrigues formula for but for
but for 
So, we have two different results. And only one of them is correct. I can’t find mistake in my calculations. But will continue searching until the issue get resolved.
Thanks. Fixed. Vector n in the note was minus that in RDEDUCE code. Code was OK. Note was incorrect. Now should be ok.