Let me start with a quote from Richard Feynman, “The Character of Physical Law“, The M.I.T. Press 1985, p. 129:
… There was a time when the newspapers said that only twelve men understood the theory of relativity. I do not believe there ever was such a time. There might have been a time when only one man did, because he was the only guy who caught on, before he wrote his paper. But after people read the paper a lot of people understood the theory of relativity in some way or other, certainly more than twelve.
On the other hand, I think I can safely say that nobody understands quantum mechanics.
While we do not understand quantum mechanic, and I am here in a complete agreement with Feynman, we (that is I) find it useful, and we find that we can learn something from it (Quantum Mechanics). We can, rightly or wrongly, get from Her (Quantum Mechanics) some glimpses of “future physics”. In fact many physicists and mathematicians are trying to knock more or less to the same door, though the door still remain closed. The door has a plate on it, and the inscription on the plate reads: Spin, complex, dimensions.

I am going to open this door, just a little, and to stick my head in, to get a glimpse of what is inside.

Inside there is certainly spin, and it is complex. So we go through the door, and enter the first office behind. There are three little Pauli matrices there. They are asking us to play with them.
We can’t refuse.
Pauli matrices are ![]() complex matrices. Here they are, happy, ready to play with, on the yellow background
complex matrices. Here they are, happy, ready to play with, on the yellow background
(1) ![]()
Two of them are, in fact, real. One is imaginary. But all three of them are Hermitian:
![]()
Where ![]() denotes the Hermitian conjugate, that is “transpose and complex conjugate”. Suppose now that
denotes the Hermitian conjugate, that is “transpose and complex conjugate”. Suppose now that ![]() is a (real) vector in our three-dimensional space. Then we can build the matrix
is a (real) vector in our three-dimensional space. Then we can build the matrix
(2) ![]()
The matrix ![]() is again Hermitian. We do not like it. We like to have anti-Hermitian matrix that we will exponentiate, much like in the previous post we were exponentiating antisymmetric matric. Since we are behind the door to a complex space, we can use imaginary
is again Hermitian. We do not like it. We like to have anti-Hermitian matrix that we will exponentiate, much like in the previous post we were exponentiating antisymmetric matric. Since we are behind the door to a complex space, we can use imaginary ![]() . There are a lot of them in every drawer. So, we choose one and exponentiate:
. There are a lot of them in every drawer. So, we choose one and exponentiate: ![]()
The matrix ![]() is unitary:
is unitary: ![]() This follows from a general formula for the exponential:
This follows from a general formula for the exponential:
![]()
Thus ![]()
There is also a complex version of the Rodrigues rotation formula that we have seen in the previous post Spin – we know that we do not know. It is a fun to derive it, so why not?
Let ![]() be a unit vector (that is of norm 1), that is
be a unit vector (that is of norm 1), that is ![]() We can calculate
We can calculate ![]() and, to our surprise, we find that:
and, to our surprise, we find that:
![]()
Since ![]() it follows that
it follows that
![]()
![]()
Now we put ![]() in front:
in front:
![]()
![]()
Calculating the exponential ![]() we can collect all even powers and all odd powers to get:
we can collect all even powers and all odd powers to get:
![]()
Or
![]()
So far so good. Complex proves to be simpler. Nature loves it! For real matrices we have three terms in the Rodrigues rotation formula. For complex matrices we have only two! So, we should really be happy. Except that we do not know yet where are these “rotations” now? That will be in the next post. But anticipating, we rewrite the formula above as
(3) ![]()
In the middle of writing this post I went for a bicycle ride. To spin my wheels. I came back and my left monitor was dead. I t just died while waiting for me. It was Samsung SyncMaster 913N. While it is true that it was already 12 years old, but i will miss him! R.I.P.

New monitor will come on Monday. In the meantime I will have only one window.




“Thus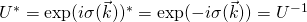 “.
“.
Why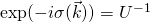 ?
?
Because of general rule
which is a particular case of
Though it is not true in general that
Unless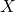 and
and 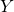 commute.
commute.
And thanks for the errata. Fixed.
That is exactly what I wanted to receive.
“właśnie zmarł, czekając na mnie. Było Samsung SyncMaster 913N”
naprawdę prosta naprawa-wymiana kondensatora
https://www.youtube.com/watch?v=JikTCaoE0Sw
Tak i myślałem. Trzy kondensatory były spuchnięte.