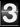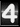To quote from Wikipedia:
Method
LaPiere travelled round America with a Chinese couple, expecting to meet discrimination as a result of anti Chinese feeling. At the time prejudice against Asians was widespread and there were no laws against racial discrimination. They visited 67 hotels and 184 restaurants. Six months later, after their return, all the establishments they had visited were sent a letter, asking whether they would accept Chinese guests.
Results
They were only refused at one of the establishments they visited, and were generally treated very politely. Of the 128 establishments which responded to the letter, 91% said they were not willing to accept Chinese guests.
Conclusion
Attitudes do not always predict behavior. Cognitive and affective components of attitudes are not necessarily expressed in behavior.
The LaPiere’s study shows that the cognitive and affective components of attitudes (e.g. disliking Chinese people) do not necessarily coincide with behavior (e.g. serving them).
Very clever are these psychologists. But we are discussing attitude matrix of the free rigid body. We did not quite finish in the last post with the case ![]() I will finish it here. First we have to go back to Standing on the shoulders of giants – Reboot, where we have introduced the new matrix
I will finish it here. First we have to go back to Standing on the shoulders of giants – Reboot, where we have introduced the new matrix ![]() I will write it here in a slightly different form:
I will write it here in a slightly different form:
(1) 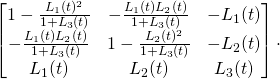
Assuming that ![]() it is a simple exercise to check that both formulas give the same result. Given the matrix
it is a simple exercise to check that both formulas give the same result. Given the matrix ![]() we can use the same method that we have used before in Taming the T-handle, find the equation for
we can use the same method that we have used before in Taming the T-handle, find the equation for ![]() , and solve it. This time solution involves elliptic function:
, and solve it. This time solution involves elliptic function: ![]() Here is the formula I have obtained using computer algebra software (I am doing copy and paste from Mathematica):
Here is the formula I have obtained using computer algebra software (I am doing copy and paste from Mathematica):
(2) 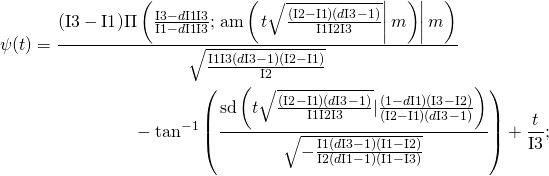
Then, in order to obtain the attitude matrix, we do the same as before. And I will continue and explain in the next post. With the new form of the attitude we will obtain exactly the same behavior as with the previous attitude. Yet for quaternions the new attitude will be much better!