In my recent post I was presenting new formulas for the attitude matrix, different from those of a month ago. And I did not explain in detail how I got them, and why they look like being in disagreement with the previous ones. This caused a legitimate concern from Bjab, when he noticed the apparent disagreement. And indeed putting new wine into old bottles would lead to a trouble.
Mar 2:21 No man also seweth a piece of new cloth on an old garment: else the new piece that filled it up taketh away from the old, and the rent is made worse.
Mar 2:22 And no man putteth new wine into old bottles: else the new wine doth burst the bottles, and the wine is spilled, and the bottles will be marred: but new wine must be put into new bottles.

What we did is this: we poured new wine into new bottles. And here is how it is done.
We consider free rigid body with normalized (unit length) angular momentum vector, and the doubled kinetic energy equal to ![]() Euler’s equations can be then solved explicitly and we choose the following solution:
Euler’s equations can be then solved explicitly and we choose the following solution:
(1) 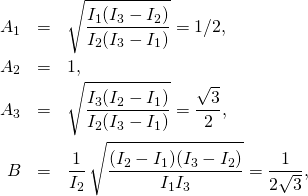
(2) 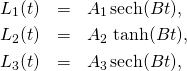
where ![]()
We will need the angular velocity vector with components
(3) ![]()
We want to solve now the differential equation for the attitude matrix ![]()
(4) ![]()
where
(5) 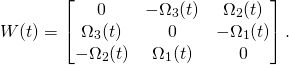
The strategy is this: We seek the solution of the form ![]() where
where ![]() is a certain matrix cleverly constructed out of
is a certain matrix cleverly constructed out of ![]() and
and ![]() is a simple rotation matrix by some angle
is a simple rotation matrix by some angle ![]()
There are two methods: old one, and new one.
The old method.
In the old method, as used for instance in Taming the T-handle continued (we use now ![]() instead of
instead of ![]() there), we set:
there), we set:
(6) ![]()
(7) 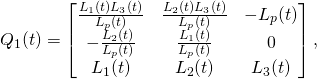
(8) 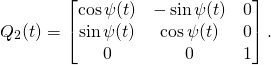
Then we solve for ![]() :
:
(9) 
The new method.
(10) 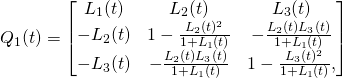
(11) 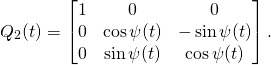
(12) ![]()
where
(13) ![]()
Comparing old and new wines
In both cases we get a solution of the attitude differential equation (4). But these are different solutions. If ![]() is a solution, and if
is a solution, and if ![]() is a fixed rotation matrix of determinant one, then
is a fixed rotation matrix of determinant one, then ![]() is another solution. This is the same body rotating, but observed from two different laboratory frames.
is another solution. This is the same body rotating, but observed from two different laboratory frames.
Let ![]() and
and ![]() be the two solutions, one obtained with the old, the other one with the new method.
be the two solutions, one obtained with the old, the other one with the new method.
With some little algebra it can be verified that ![]() where
where
(14) 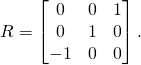
.
Therefore for all ![]()
(15) ![]()
I verified it numerically. The above comparison was for rotation matrices. For quaternions it is similar, though the quaternion case deserves a comment. I will give it in another note.


