It was yesterday that I started writing about the idea of more than one path. I imagine being a rigid body in zero gravity. I mean not like a dead human body floating in cosmic space, rather like the T-handle experiencing Dzhanibekov effect. I am floating in space.

How does it feel being a T-handle? My space is the three-dimensional rotation group. Perhaps the group of unit quaternions, the sphere . My perception, perhaps, projects it stereographically on 3-dimensional space, so it is much like for me, the human being thinking about being the T-handle. But, according to the analysis from yesterday’s post More than one path, my sky has two sets of privileged directions. If I start moving into such a privileged direction, very soon I will be close to performing eternal returns moving along essentially always the same circle.

But will it be the same circle for each of these special lines? Or they will be different circles? How do they look? These special trajectories? I am trying to figure it all out, and today I am reporting on my progress. It is all preliminary, there may be errors, perhaps my reasoning has mistakes? With time, and with help of my readers, I am sure we will get to the truth. So, here is what I think, and what I did because of my thinking.

Yesterday I was analyzing paths through the point -1. But, after some thinking and experimenting I decided that I do not like this point. We already have a very nice path, described by nice formulas, for instance in Meeting with remarkable circles

The path in unit quaternions at passes through the point This point is in the middle between the two circles of eternal return. There is nothing wrong with this point. Therefore I want to consider all special paths that have the property that at they pass through this point. This is my task.
So, I went to work, and now I will show you the result. Which may be right, or may be wrong – I do not know yet. First pictures, then explanation how I got them:

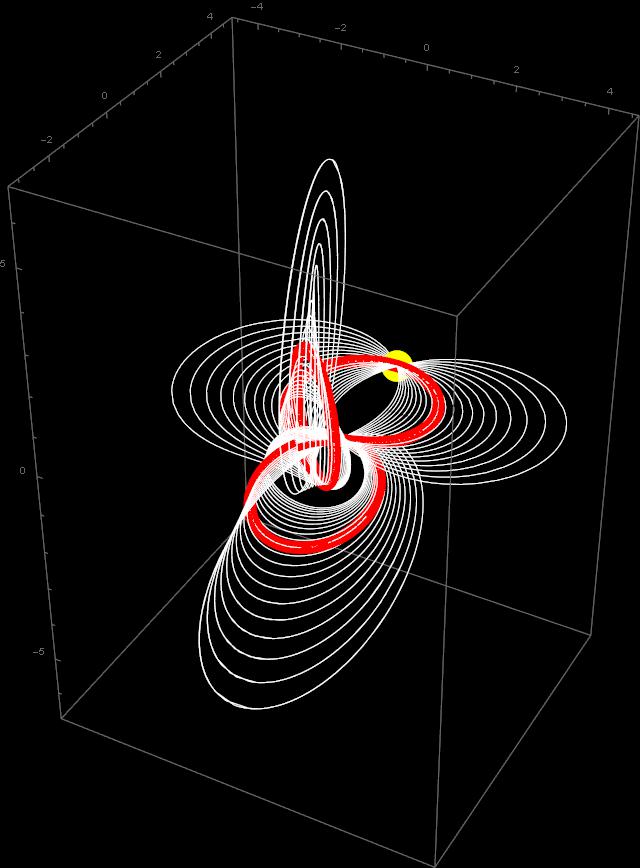
The yellow point is the common starting point The red path is the same as in the picture before, the path that we already know. The other paths are also special, starting at the same point, but in different special directions. There are only 21 of them – to start with. What we are getting is something similar to a butterfly. It would not, probably, be able to fly in 3D, but it may be able to fly in 4D. If you click on the butterfly image animation will open showing it from different angles, so that you can get a better idea about its space structure.

Perhaps our souls, when flying, look like that?

How did I get it? I decided that other special paths I will get choosing other solutions of the same Euler’s equations. To choose a different solution I shifted time in the solution for (I did not play with signs yet). This way I get a different solution of the attitude equation. But this new solution has a different starting point. So I multiply by a constant quaternion from the left to move the starting point to above.
I did not shift time too much, just with spacing so I got 21 trajectories.
Now I have to check all that and, if necessary, fix what needs to be fixed.
When all is fixed, I will share the code.