
Far out in the uncharted backwaters of the unfashionable end of the Western Spiral arm of the Galaxy lies a small unregarded yellow sun.
Orbiting this at a distance of roughly ninety-eight million miles is an utterly insignificant little blue-green planet whose ape-descended life forms are so amazingly primitive that they still think digital watches are a pretty neat idea.
This planet has—or rather had—a problem, which was this: most of the people living on it were unhappy for pretty much of the time. Many solutions were suggested for this problem, but most of these were largely concerned with the movements of small green pieces of paper, which is odd because on the whole it wasn’t the small green pieces of paper that were unhappy.
And so the problem remained; lots of the people were mean, and most of them were miserable, even the ones with digital watches.
So sets Douglas Adams the scenery in his Hitchhiker’s Guide to the Galaxy. And he is right, neither green pieces of paper nor digital watches will make us happy. But digital computers – that’s another story. Digital computer, with some patience and determination made me happy today (or I made him happy, doesn’t mater which way), and I am going now to share my happiness with you. Because there is no true happiness which is not shared happiness.
And no, I am not going to calculate the answer to the Ultimate Question of Life, the Universe and Everything. Though we will be not very far away from obtaining such an answer. But please, don’t panic!

In the last post I have perversely asked this question:
So, my guess is that the formula (23) in the paper has wrong signs. What to do?
Should I write to the authors?
Now I admit, I was not completely sincere. I was teasing, I was playing with You, the Reader. Because the truth it that months ago I discovered wrong signs in the formula (20) of this paper. So, being young and naive, I wrote to prof. Zanna announcing my discovery. Here is the reply I got:

So, we should not consider the paper as being sacred, typos sometimes happen. But software – that is something different. Software is a serious matter. The software has been thoroughly tested, so if we test our software against something that has been thoroughly tested, that will be even better than through tests of our own code!
In The Hitchhiker’s Guide to the Galaxy the answer came as forty two.
“I checked it very thoroughly,” said the computer, “and that quite definitely is the answer.
We will also check very thoroughly. Our answer will not exactly be forty two. But we will come out with a quaternion, quaternio, quatro – it can explain 4. It remains to explain the last 2.
We will be testing example four from the code 903 – you need to read a couple of previous posts if you do not know what I am talking about. Alternatively, you can download the file 903.zip, unzip it, go to the folder 903\Fortran77\Drivers, and contemplate the following three files there: driver_example4.f, init_example4.dat, out_example4.dat. All three with number four. That is what we will be doing now.

According to README.txt
driver_example3.f (example for FRB integration with many steps
of lenght h from 0 to Tfin, using
semi-exact methods)
To be linked with frb_step.f
driver_example4.f (Like driver_example3.f but uses quaternions)
To be linked with quat_step.f
Both examples have the body with the same moments of inertia, but initial momenta are different. So it is impossible to compare their outputs. We return to this issue later on, for now let us concentrate on example4.
The moments of inertia can be read from init_example4.dat. They are
(1) 
So it is the same “future physics” body that we have already met in , when discussing example2.
Then comes initial angular momentum (which sometimes I call ![]() and sometimes
and sometimes ![]() :
:
(2) 
As in Spinning Gulliver among giants we have
(3) ![]()
We calculate ![]()
![]()
So ![]() therefore we have
therefore we have ![]() case.
case.
Now I am presenting the complete ![]() algorithm based on the method introduced in Standing on the shoulders of giants – Reboot.
algorithm based on the method introduced in Standing on the shoulders of giants – Reboot.
(4) 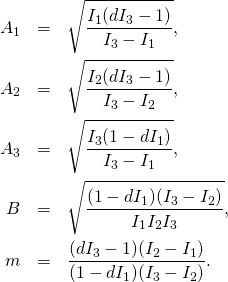
The solution ![]() of the Euler’s equations has two trajectories: one with
of the Euler’s equations has two trajectories: one with ![]() is given by
is given by
(5) 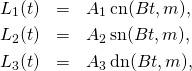
while the other one, with ![]() is given by
is given by
(6) 
With constants ![]() and
and ![]() defined as
defined as
(7) 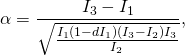
(8) ![]()
we set the phase variable ![]() as
as
(9) ![]()
where the Jacobi function ![]() is defined as
is defined as ![]()
Then the quaternionic attitude solution is given by ![]() with
with
(10) 
My original intention was to verify the above with the 903 paper code using Mathematica, and, if there will be differences in the output, to fix the problems.
But now this Sunday is coming to the end, and I am getting tired. And before sleep I want to watch the second half of the movie “Master and Commander”. It fits this post:

Roger Ebert gave the film 4 stars out of 4, saying that “it achieves the epic without losing sight of the human”




Is m1(0)=L1(0) etc?
these are the values I get
t0 := 0;
m10 := L1(t0);= 0.90464553008
m20 := L2(t0);=0
m30 := L3(t0); =0.6471867488337
sqrt(L1(t0)^2+L2(t0)^2+L3(t0)^2);=1.112310308
sqrt(-.544332842^2+.7291317^2+(-.414811526^2));
= 0.25152794647743 (i.e the values from the paper)
I thought the magnitude of L or m should be 1
Things could also get a bit confusing with m for the Jacobi functions (even though I use k) and m for angular monentum.
Just to make sure I am not totally confused
Q0 is the Rodrigues / Quaternion Matrix
Q1 is the [cos (psi) -sin (psi) 0……] Matrix
Q is Q1.Q0
Have lots of numerical issues here. Magnitued of the determinant of Q0 is changing.
I am getting.
L3[0] = -0.426165
But I did not yet give the formulas fro Q0,Q1 and Q. They will come.
“So it is the same “future physics” body that we have already met”
Did the authors tell a word that they were especialy dealing with “strange” rigid body?
No. I guess as a test for the software it is quite ok. For instance there is nothing wrong in having negative mass in Newton’s equations. Mathematics is the same.
Thanks for the errata.
Ark
In the meantime.
Would you please show me the graph of a functon: angle(time)?
Where:
angle is the angle between the velocity vector of the end of leg of T-handle and XY-plane of T-handle
(or angle is the angle between the velocity vector of the end of leg of T-handle and the vector perpendicular to XY-plane of T-handle)
In two cases:
Case 1
m=1.000001
Case 2
m=0.999999
OK. It will take a while.
Angle with z axis in degrees
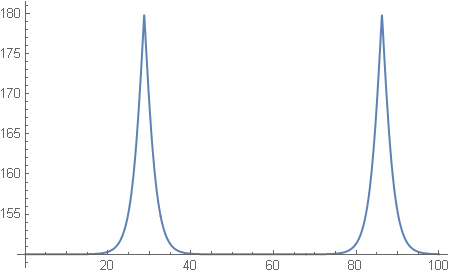


Case 1
m=1.000001
Case 2
m=0.999999
Case 3
m=1.0
Thank you for the graphs.
I have to interpret them now.
I don’t understand them.
(Haven’t you exchanged cases 1 and 2?)
They were completely wrong. I do not understand how it happened. Something weird. Replaced them. But I am not yet 100% sure I got them right this time.
Please restore former graphs. Now I think they were correct. (I don’t like new graphs a lot.)
I agree. Did them again, from scratch, and they seem to be OK.
So from the shape of graph of Case 2 (m=0.99999) we can conclude that Case 2, in the limit, becomes Case 3 (m=1) splited into two cases:
Case 3a:
m=1 and angle = 150 (shown on the graph) and
Case 3b:
m=1 and angle = 30 (not shown).