I noticed that somehow I did not finish with the case ![]() So today, without further ado, I am posting the algorithm.
So today, without further ado, I am posting the algorithm.
We have the body with ![]() and we are considering the case with
and we are considering the case with ![]() , where
, where ![]() is, as always, the ratio of the doubled kinetic energy to angular momentum squared.
is, as always, the ratio of the doubled kinetic energy to angular momentum squared.
Then we define
(1) 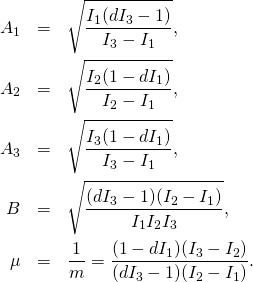
(2) 
(3) 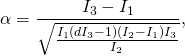
(4) ![]()
(5) ![]()
(6) 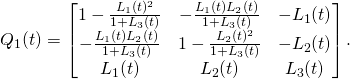
(7) 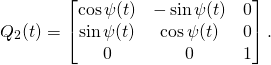
(8) ![]()
(9) 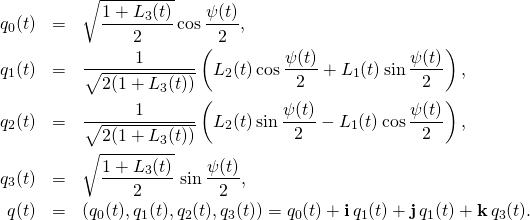
I use the above formulas to draw a stereographic projection of one particular path. So, I take ![]() , and do the parametric plot of the curve
, and do the parametric plot of the curve ![]() in
in ![]()
with
![]()
I show below two plots. One with ![]() and one with
and one with ![]() For this selected value of
For this selected value of ![]() the time between consecutive flips, given by the formula
the time between consecutive flips, given by the formula
(10) ![]()
So, for ![]() we have somewhat less than 200 flips, and the lines are getting rather densely packed in certain regions.
we have somewhat less than 200 flips, and the lines are getting rather densely packed in certain regions.
Notice that is just one geodesic line, geometrically speaking the straightest possible line in the geometry determined by the inertial properties of the body.
It is this “geometry”that will become the main subject of the future notes.
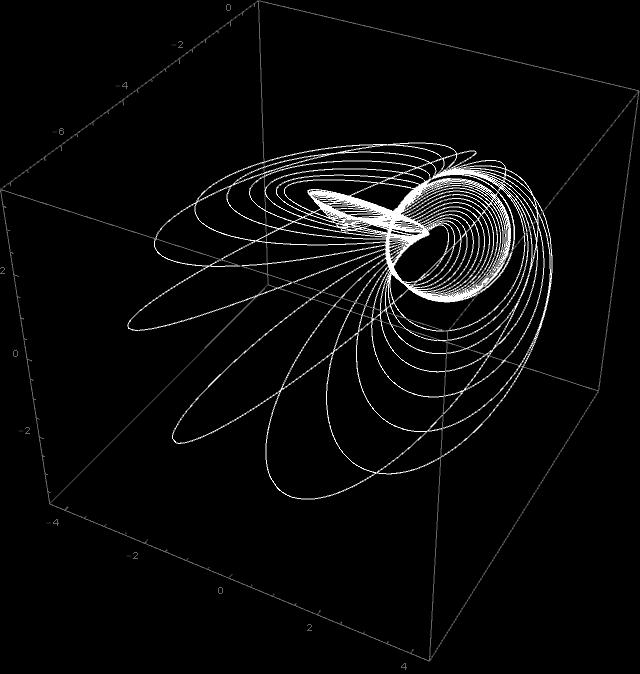

How can such a line be “straight”? Well, it is….



I noticed, on this 10000 picture, that there appears something similar to Saturn’s rings. Don’t know why. Perhaps it is a numerical artefact, but perhaps it is a real thing! A DISCOVERY?
It is not surprising – for some d’s the path should be closed.
I mean closed and relatively short.
What i was plotting is just one trajectory. I mean in theory, because taking into account numerical approximations who knows what I was plotting in reality?
In the meantime I have made the plot increasing time from 10 000 to 100 000. It came out completely dense without any Saturn’s rings structure. But numerically it is even less reliable.
Yes, some trajectories are exceptional, but how easy it is to spot such is not an easy question to answer – except of the three uniform rotations about inertia axes.
Have you made pictures (also with time 10 000) but with d slightly greater and d slightly less than already shown 0.5000001 ?
I suspect that small variation in d should thighten or loosen the “Saturn’s rings”.
I did some tests. With no clear conclusions. For instance for d=0.5000002 there are groups of 2 instead of 5 as in the pisture in the post.
So the variation (0.0000001) was too big.
Can you post a couple of values for psi(t) as a check please. I get
psi(7)=5.010163143
psi(179)=163.1996033
For d=0.5000001 Mathematica gives me
psi(7)=3.09517
psi(179=98.0193
I will try now to reproduce these values with Maple
Here is my Maple code. Result agree. Perhaps you have forgotten to take square root of mu?
I1 := 1.0; I2 := 2.0; I3 := 3.0; d := .5000001; A1 := sqrt(I1*(I3*d-1)/(I3-I1)); A2 := sqrt(I2*(-I1*d+1)/(I2-I1)); A3 := sqrt(I3*(-I1*d+1)/(I3-I1)); B := sqrt((I3*d-1)*(I2-I1)/(I1*I2*I3)); mu := (-I1*d+1)*(I3-I2)/((I3*d-1)*(I2-I1)); kappa := sqrt(mu); nu := (-I1*I3*d+I3)/(-I1*I3*d+I1); alpha := (I3-I1)/sqrt(I1*(I3*d-1)*(I2-I1)*I3/I2); epi := proc (t::float, nu::float, k::float) local t2, n, dt, ep0, res; ep0 := EllipticPi(nu, k); t2 := EllipticK(k); n := floor(t/t2); dt := t-n*t2; if type(n, even) then res := Re(n*ep0+EllipticPi(JacobiSN(dt, k), nu, k)) else res := Re((n+1)*ep0-EllipticPi(JacobiSN(t2-dt, k), nu, k)) end if end proc;
1.0
2.0
3.0
0.5000001
0.5000001500
0.9999999000
0.8660253172
0.2886752212
0.9999992000
0.9999996000
-2.999997600
2.309400384
proc(t::float, nu::float, k::float) … end;
psi(t):=t/(I3)-arctan((A2/(A1))*JacobiSD(B*t,kappa))+alpha*epi(B*t,nu,kappa);
t /A2 JacobiSD(B t, kappa)\
t -> — – arctan|———————–|
I3 \ A1 /
+ alpha epi(B t, nu, kappa)
psi(7);
3.095170587
psi(179);
98.01928537
Thank you. My problem was in alpha. Things agrees now. Oh I ommited to say d=0.6
I get strange kicks in the path. http://imgur.com/RIoHWha . My quaternion for t =179 evaluates to
Vector[column](4, [0.8808818313e-1, .1154559730, -.8474014431, .5107065531])
Cheching the quaternion formula, it is the negative of what you have posted in the formulas.
Is that for d=0.6?
“Cheching the quaternion formula, it is the negative of what you have posted in the formulas.”
Which formulas?
I have to improve my communication level.
Lets take d=0.6 t=179
Your quaternion formula (9) evaluates to
Vector[column](4,
[-.6452072055, .2607319986, .5511334836, -.4604110882])
Stereographicially projected above evaluates to
Vector[column](3, [.1584797329, .3349933562, -.2798499098])
The quaternion I arrived at evaluates to
Vector[column](4,
[.6452072054, -.2607319985, -.5511334835, .4604110882])
Stereographicially projected evaluates to
Vector[column](3, [-.7348852696, -1.553395367, 1.297690075])
Appears very different in 3D.Interestingly similar but different paths are produced.
See the plots in link
There are twice as many lines in the combined plot as the paths don’t match.
http://imgur.com/a/Vhy9q
That is, communicationwise, better. But I do not know which way you got your numbers?
This is a download link for the work sheet
https://www.dropbox.com/s/ibslbd2vh26r9wg/076-Attitude%20Matrix%20and%20Quaternion%20path%20for%20m%20greater%20than%201.mw?dl=0
Shows how I arrived at my results.
Looking at your file I am finding:
My derivation.
` This is from Algorithm 903 paper and post:- Giants that Stumble`;
q1(t):= 1/(sqrt(2)) Vector(4,[-sqrt(1+L3(t)),-(L2(t))/(sqrt(1+ L3(t))),(L1(t))/(sqrt(1+L3(t))) ,0]);
Where did you get this formula from? It is the minus of what is in the paper, and what is in my formula.
Now I remember/know. In giants that stumble and the paper I didn’t understand where the quaternion came from. Figured out how to derive the individual ones to rotate to x,y & z axis. You had mentioned a problem with incorrect “-” signs causing a mess. I realised a negative quaternion can also be used to achieve the rotation.http://arkadiusz-jadczyk.eu/blog/2017/03/giants-stumble/#comment-671. I guess I never changed the signs back then copy pasted to recent worksheet.
Lesson here just because the negative unit quaternion produces the same rotation, it does not produce the same sterographic projection.
Yes. I have chosen stereographic projection from the pole +1. I could have chosen from -1. Then minus quaternion projected from +1 is negative of + quaternion projected from -1.