You look like an angel
Walk like an angel
Talk like an angel
But I got wise
You’re the zero in disguise
Oh, yes, you are
The zero in disguise
Elvis was singing about you ….
Ronan, in his recent comment under my post on Quaternion evolution, has noticed that Maple, the software he is using, gives for the function ![]() result that than the one I was advocating. How can it be? Mathematics is an exact science (physics, on the contrary, is not exactly an exact science). For a given question there should be one answer. Or is mathematics a devil in disguise? Looks like an exact science, walks like an exact science, but exact science it is not?
result that than the one I was advocating. How can it be? Mathematics is an exact science (physics, on the contrary, is not exactly an exact science). For a given question there should be one answer. Or is mathematics a devil in disguise? Looks like an exact science, walks like an exact science, but exact science it is not?
Devil likes to hide in the details, so let us examine the details.
My formula for ![]() comes from integration. I claim that if we integrate
comes from integration. I claim that if we integrate
(1) 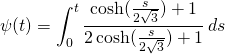
the result is given by rather simple a formula:
(2) 
Ronan, who is using Maple, gets for the same problem a different answer:
(3) 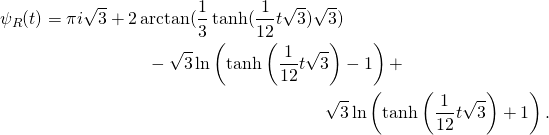
Taking the difference we get
(4) 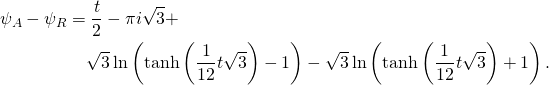
If mathematics is not a devil in disguise, the last expression, namely ![]() must be a zero in disguise. But is it?
must be a zero in disguise. But is it?
I tried to ask Maple to simplify it, with no result. The algorithms known to otherwise very clever software are not smart enough. So, let is see what we can do with our eyes and hands.
The first thing that comes to our attention is that we have a difference of logarithms. And we know from the kindergarten that ![]() So we write
So we write
(5) 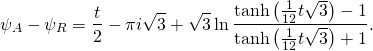
But what is ![]() ? We know that
? We know that ![]() therefore
therefore
(6) 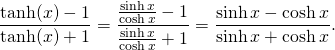
Now, ![]() therefore
therefore ![]()
![]() Thus
Thus
![]()
and so
![]()
We can write now
![]()
What is ![]() ? It is an imaginary number. We know that
? It is an imaginary number. We know that ![]() and if we ask Maple what is
and if we ask Maple what is ![]() ? – the answer is
? – the answer is ![]() So, we finally get
So, we finally get
![]()
In our case ![]()
![]()
In Eq. (5) we have ![]() in front of the
in front of the ![]() , so we get
, so we get
![Rendered by QuickLaTeX.com \[\sqrt{3}\ln\frac{\tanh\left(\frac{1}{12}t\sqrt{3}\right)-1}{\tanh\left(\frac{1}{12}t\sqrt{3}\right)+1}=-\frac{t}{2}+\sqrt{3}i\pi. \]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-59bf80559282e701479d54bb4028d116_l3.png)
Thus ![]() The zero has been cleverly disguised using functions
The zero has been cleverly disguised using functions ![]() and
and ![]() . Einstein once commented that God is subtle, but He is not malicious. Well, here we could see Mathematics can be subtle
. Einstein once commented that God is subtle, but He is not malicious. Well, here we could see Mathematics can be subtle




Wow. I didn’t expect this tonight. Thank you. Amazing how different softwares work. I was all set to dive into simplifying. Instead this enabled me do do a great deal of error checking and correcting. I now have the code for http://arkadiusz-jadczyk.eu/blog/2017/03/quaternions-you-eat/
post working properly as it agrees with yours.
Tried a general solution for the diff eqn. It actually worked be setting .
Edit:-General solution means,not giving I1,I2 and I3 numetical values. Had to define d=1/I2 and k=1.
I noticed that in “Quaternion evolution” occured an update – the blue box.
There (at the bottom) two twos missed in action.
They are back. Thanks.
“They are back”
But the first one suffers a little power.
Power restored. Thanks.
Thanks.
Found something interesting during the week when trying to solve for d not = 1/2. Convert the equation to partial fraction (d=1/2) and you get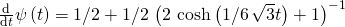 this solves nicely to
this solves nicely to