Our second field expedition

Posted on 2017/03/28 by arkajad

Our first field expedition was not without adventures. What kind of adventures they were – this can be now only guessed looking at some cryptic comments. They refer to the text that does not exist any more. I have changed the example. Last night Goddess talked to me in my dream, and She suggested a different avenue from that that I have had in my mind before. I obey. And so the second example follows. Very similar to the previous one, just a little been different.

Last time I considered the one parameter group of transformations defined, on the complex plane, by

    \[f_t:z\mapsto \frac{\cosh(t)z-i\sin(t)}{i\sinh(t) z+\cosh(t)},\]

where t\in\mathbf{R}.

Today I propose a variation:

    \[g_t:z\mapsto \frac{\cosh(t)z+\sinh(t)}{\sinh(t) z+\cosh(t)}.\]

Again, with some little effort (perhaps easier than it was before, because now there is no more imaginary i explicitly in the formula) we can verify that

g_{t+s}(z)=g_t(g_s(z)) and g_0(z)=z.

In order to obtain the vector field from this “flow of complex numbers” I am calculating the derivative:

    \[Y(z)=\frac{d}{dt} g_t(z)|_{t=0}.\]

I used Mathematica to get

    \[Y[z]=1-z^2.\]

To draw this vector field on the (x,y) plane I write z=x+iy, and calculate

    \[1-(x+iy)^2=1+y^2-x^2-2ixy.\]

So

    \[ Y(x,y)= (\mathrm{Re} (Y(z)),\mathrm{Im}(Y(z))=(1+y^2-x^2,-2xy).\]

Here is the vector field, and stream lines from this second field expedition


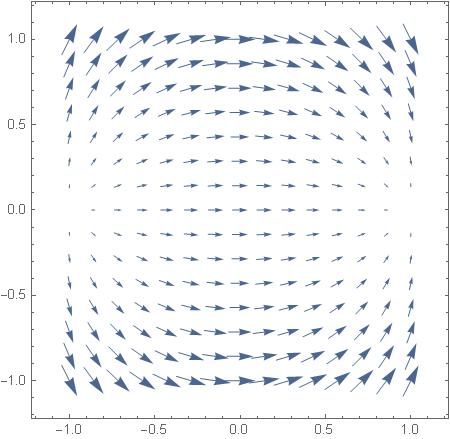
Of course there will also the third expedition. After that the mystery will slowly be be revealed.

Print 🖨 PDF 📄 eBook 📱
This entry was posted in Geometry, Mathematica. Bookmark the permalink.

4 Responses to Our second field expedition

  1. Bjab says:
    2017/03/28 at 19:28

    Arku,
    na Boga, z jakich annałów wyciągnąłeś ten pierwszy wzór z plusem w liczniku?

  2. Bjab says:
    2017/03/28 at 19:31

    Of course there will also the third expedition. After that the mystery will slowly revealed. ->
    be be

Leave a Reply