This is not an independent post or note or whatever. It is a continuation. In fact it is the continuation of Approaching the ultimate answer for m<1. We have approached enough. We are ready.
There was a moment’s expectant pause while panels slowly came to life on the front of the console. Lights flashed on and off experimentally and settled down into a businesslike pattern. A soft low hum came from the communication channel.
“Good morning,” said Deep Thought at last.
“Er … good morning, O Deep Thought,” said Loonquawl nervously, “do you have … er, that is …”
“An answer for you?” interrupted Deep Thought majestically. “Yes. I have.”
The two men shivered with expectancy. Their waiting had not been in vain.
“There really is one?” breathed Phouchg.
“There really is one,” confirmed Deep Thought.Douglas Adams, The Hitchhiker’s Guide to the Galaxy
We did not get to the answer yesterday, but today is the day. We will be using the formulas from the last post. Here they are again, repeated for your convenience:
(1) 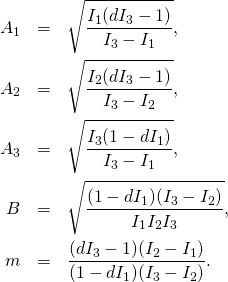
The solution ![]() of the Euler’s equations has two trajectories: one with
of the Euler’s equations has two trajectories: one with ![]() is given by
is given by
(2) 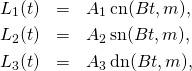
while the other one, with ![]() is given by
is given by
(3) 
With constants ![]() and
and ![]() defined as
defined as
(4) 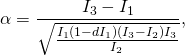
(5) ![]()
we set the phase variable ![]() as
as
(6) ![]()
where the Jacobi function ![]() is defined as
is defined as ![]()
Then the quaternionic attitude solution is given by ![]() with
with
(7) 
We consider Example Four with
(8) 
(9) 
![]() is negative, the therefore we take option as in Eq. 3). We calculate
is negative, the therefore we take option as in Eq. 3). We calculate ![]() that reproduces the initial angular momenta. The method is known from the previous posts:
that reproduces the initial angular momenta. The method is known from the previous posts:
(10) ![]()
(11) ![]()
So we have ![]() At
At ![]() our angular momentum is the same as angular momentum in example 4 at
our angular momentum is the same as angular momentum in example 4 at ![]() We calculate
We calculate ![]() from Eq'(7)
from Eq'(7)
![]()
(12) 
thus
(13) ![]()
We verify that we have indeed a unit quaternion:
![]()
Thus the inverse quaternion is the same as conjugated one:
![]()
In the Example 4 the initial quaternion, at ![]() is
is ![]() . Therefore in order for our solution to reproduce the initial data of the example we set
. Therefore in order for our solution to reproduce the initial data of the example we set
(14) ![]()
The final time in Example 4 is ![]() Therefore we calculate
Therefore we calculate
(15) ![]()
where the multiplication is the quaternion multiplication.
Calculated with Mathematica the answer is
(16) 
The result from the Fortran code in the file out_example4.dat is
-0.3676198430772359
-0.6306293413288832
-0.6127232632258010
0.3028737154869889

It seems that therefore that we have obtained the ultimate answer. At least for quaternions. We need to get it also for rotation matrices. So the saga will continue.




Something fishy
Yes, something fishy is going on.
The new algorithm, presented here, though it seems to agree with 903 code, it is not in agreement with my old algoritm for quaternions. For large t they produce certainly different numbers.
I have no idea why.
To debug the universe I will have ro start with rotation matrices rather than quaternions, which are somewhat exotic species.
So the next post will be about the new algorithm with rotation matrices, and then I will start the debugging hearing in the Congress.
Maple’s EllipticF is it defined differently to Mathematica?
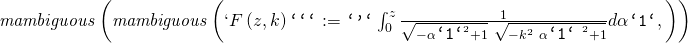
from Spinning Gulliver among giants you calculate 14.9607 is got 5.975-12.471i.
Today a got a real number but now yours.
Edit:-
Latex got messed up a bit but it shows the function. Basicially F(z,k) goes to infinity just after 5 pie /16 and doesn’t become real again.
Did a bit of research found this inMaple help
“It is worth noting the difference between the Legendre normal form of the Incomplete Elliptic integral of the first kind (see A&S 17.2.7), in Maple represented by EllipticF(z,k) but for the splitting of the square root in the denominator of the integrand (see definition lines above), and the normal trigonometric form of this elliptic integral (see A&S 17.2.6), in Maple represented by the InverseJacobiAM function
InverseJacobiAM(phi,k);
InverseJacobiAM(phi, k)”
Gives both answers for t0, 14.9607 and todays 3.17243
Problem solved. New problem:-
psi(t) is probably causing an issue.
Can you give the value for psi(t0) along with the arctan and EllipitcPi functions in it please?
Must sleep now.
The following gives the same answer as Mathematica
I1 := 1.0; I2 := 1.012686988782515; I3 := 3.306237422473038; d := .8733147046233154; m := (I3*d-1)*(I2-I1)/((-I1*d+1)*(I3-I2)); k := sqrt(m);
A2 := sqrt(I2*(I3*d-1)/(I3-I2)); A3 := sqrt(I3*(-I1*d+1)/(I3-I1)); alpha := (I3-I1)/sqrt(I1*(-I1*d+1)*(I3-I2)*I3/I2); nu := (-I1*I3*d+I1)/(-I1*I3*d+I3); B := sqrt((-I1*d+1)*(I3-I2)/(I1*I2*I3)); t0 := 3.17243;
psi(t):=t/(I1)-alpha*epi(B*t,nu,k)-arctan((A2)/(A3)JacobiSD(B t,k));
psi(t0);
0.838675316
Thank You Ark,
Fixed the problem.
Ark,
I see that signs of Z in (12), (13) and below are inconsistent.
I have forgotten minus in (12). Fixed. Thank you.
Can you explain this formula please?
Don’t understan it? But then I would need you to explain why we need a spacial t_0. What is wrong with 0 or why would zero be wrong?
A general solution of equations of motion involves integration constants that would allow accomodating arbitrary initial conditions. We do not have such constants, so we accomodate initial data in a different way. First we need to have correct angular momenta. For this we are shifting our solution by t0. Then we need to take into account initial q. For this we shift the shifted solution by multiplication from the left by
If we would set
then we would have satisfied, but that would be a solution with wrong initial angular momenta (that is, it would correspond to a different initial values of
satisfied, but that would be a solution with wrong initial angular momenta (that is, it would correspond to a different initial values of  ).
).
If the above is not clear, please let me know, and I will will elaborate more.
Edit- copy paste of letex script hasn’t worked.Removing $ signs worked but doesnt directly display equation.
My basic question concerned http://quicklatex.com/cache3/ce/ql_39e56426e65caff39b00d673d49df4ce_l3.png
That deals with quaternion “logic”. So far I only have a rudimentry level of knowlege of them. It is a tough situation even to figure out the revelant question to ask. I don’t want to waste you time.
So 2 questions,
1) If it is not to time consuming to explain,I would appreciate you pointing me to a reference that explains why you need to multiply by q(0)^-1 intoq(t+t0).
2) What does the ~ over q(t) actually indicate/mean/represent.
Oh. Latex gone mad and didn’t give me time to edit it.
You used both dollar and begin equation in one formula. Dollar is for inline formulas, begin equation for numbered displayed ones.