Without knowing it, during the last three posts (Our first field expedition, Our second field expedition, The Third Expedition) we became hyperbolic. Hyperbolic and conformal. Conformal and relativistic, relativistic and non-Euclidean.
How so?
It will take us a while to get accustomed to these terms and, moreover, there is no good systematic way of progressing. So, we will progress in a somewhat haphazard way – that is the natural way.
The three streams that we had seen in three recent notes have one thing in common: they all map the unit disk of the complex plane into itself. Here are again these streams, but now, with the unit disk marked up:

I do like disks. Throwing a disk so that it would fly really far,and in the intended direction, is an art.

The three one-parameter transformation groups and their vector fields that we have met are
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
Looking at the pictures of flows it is not completely clear that ![]() and
and ![]() indeed map the disk into itself. For
indeed map the disk into itself. For ![]() it is not clear from the picture what happens to
it is not clear from the picture what happens to ![]() at the bottom of the disk. and for
at the bottom of the disk. and for ![]() it is not clear what happens to
it is not clear what happens to ![]() at the right. But we can easily calculate from the equations that
at the right. But we can easily calculate from the equations that ![]() for all
for all ![]() and, similarly,
and, similarly, ![]() for all
for all ![]()
So ![]() is the fixed point of
is the fixed point of ![]() and
and ![]() is a fixed point of
is a fixed point of ![]() (The disk origin
(The disk origin ![]() is a fixed point of
is a fixed point of ![]() ) Yet the fact that
) Yet the fact that ![]() and
and ![]() map the unit disk onto itself (and the unit circle onto itself) is not completely evident and needs a proof, that is if one wants to know rather than to believe. We will return to this problem later on, in the future posts. For now there are more urgent questions:
map the unit disk onto itself (and the unit circle onto itself) is not completely evident and needs a proof, that is if one wants to know rather than to believe. We will return to this problem later on, in the future posts. For now there are more urgent questions:
What it has to do with hyperbolic, conformal, relativistic and non-Euclidean? Hyperbolic – we can partly guess: there are hyperbolic functions in the formula. But what they have to do with hyperbolas? Conformal? Our transformations preserve angles, but that is not evident. Relativistic? Once we know why hyperbolic, we will start to understand about being relativistic and non-Euclidean.
To start with, let me tell you right away how I got these formulas. First, I will tell it without explaining and/or elaborating. I will explain the details and steps later on.
I do like the groups SU(2,2) and its baby version SU(1,1). Here I am using SU(1,1) – the special unitary group for signature ![]() . This is the group of all
. This is the group of all ![]() complex matrices
complex matrices ![]() of determinant one,
of determinant one, ![]() that have the property that
that have the property that
(7) ![]()
, where
(8) ![]()
and star ![]() is Hermitian conjugated matrix to
is Hermitian conjugated matrix to ![]()
If ![]() is a path in SU(1,1) through identity,
is a path in SU(1,1) through identity, ![]() then, by differentiating the defining equation
then, by differentiating the defining equation
(9) ![]()
(10) ![]()
Now, if
![]()
then, from the condition ![]() it follows that
it follows that ![]() that is
that is ![]() Then for
Then for ![]() we get
we get
![]()
and from Eq. (10) we get ![]() and
and ![]() Thus
Thus ![]() is of the form
is of the form
(11) ![]()
where ![]() is real and
is real and ![]() is complex. This is the Lie algebra of the group SU(1,1). I first take its generator
is complex. This is the Lie algebra of the group SU(1,1). I first take its generator
(12) ![]()
I exponentiate (using, for instance, Mathematica, but by hand it is also easy, once you notice that ![]() :
:
(13) ![]()
My prescription for acting with ![]() complex matrices on complex numbers is via linear fractional transformations. Thus if
complex matrices on complex numbers is via linear fractional transformations. Thus if ![]() is of the form
is of the form
(14) ![]()
then it acts on complex numbers as
(15) ![]()
That is how I arrived at ![]() Doing the same for
Doing the same for ![]() I got
I got ![]() , and with
, and with ![]() I obtained
I obtained ![]()
That was a short summary. With time it will all become clear. Little by little it will also becoming clear what is, or can be, the relation of these
games with matrices to spinning tops and Dzhanibekov’s T-handles. In short: I am interested in relativistic T-handles. That is when not only space but also time are set in motion. It is kinda futuristic, but that is why it is fun to do it.





“from the condition it follows that
it follows that  ,”
,”
How?
This is general, but in two dimensions it is simple indeed.
Let
Then
Suppose for all
for all  That is
That is

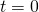 and take into account that
and take into account that  that is
that is  and
and  You find that
You find that 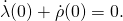
Differentiate at
Thanks!
“I first take its generator”
Generator – what is it?
its generator – whose generator?
In short: elements of the Lie algebra are called “generators”. They generate on-parameter subgroups through exponentiation.
Lie algebra of a Lie group: tangent space at identity, equipped with the commutator. For matrix group it is simply a linear space of matrices with certain linear properties that are inherited from the group definition, as exemplified in the note.
How did you get from eq (14) to eq (15)? Why is it so?
That was derived only in
http://arkadiusz-jadczyk.eu/blog/2017/04/su11-action-disk/
But it will be also discussed in future posts.