On one hand we easily find this kind of an advice:
Is it possible to follow more than one path?
If you are practising spiritual discipline under the guidance of a Master, it is always advisable to give up your connection with other paths. If you are satisfied with one Master but are still looking for another Master, then you are making a serious mistake.
On the other hand we find this
Be All You Can Be: Don’t Choose One Path, Choose Multiple Paths
We will follow the second option, we will look for other paths, other than the one we already know. Other but of the same quality
This project has two parts. The first part is pure algebra. No pictures. Pictures will come in the second part, when we will already know what to picture.

Consider this scenario: we are looking at all possible trajectories of the dynamics of our free rigid body with ![]() in the quaternion group
in the quaternion group ![]() Consider all trajectories
Consider all trajectories ![]() with the property that
with the property that ![]() Or, better, with the property that
Or, better, with the property that ![]() Why
Why ![]() is better? Because under stereographic projection
is better? Because under stereographic projection ![]() is mapped into infinity, while
is mapped into infinity, while ![]() is mapped into the origin of the coordinate system. Easier to draw.
is mapped into the origin of the coordinate system. Easier to draw.
From our point ![]() the trajectory can go in any direction. The direction of the trajectory is described by the derivative
the trajectory can go in any direction. The direction of the trajectory is described by the derivative ![]() We know that every trajectory is a solution of the equation
We know that every trajectory is a solution of the equation
(1) ![]()
Therefore, since ![]()
(2) ![]()
Let us assume that the angular momentum vector is normalized, it has unit length. We are interested in those very-very special trajectories for which ![]() They are special, they encode the essence of the flip in Dzhanibekov effect. In what follows, to simplify the notation I will write
They are special, they encode the essence of the flip in Dzhanibekov effect. In what follows, to simplify the notation I will write ![]() instead of
instead of ![]()
The doubled kinetic energy is
(3) ![]()
The length of the angular momentum vector, assumed to be 1, is
(4) ![]()
We want our path to be special, that is we want ![]()
Eq. (3) gives then
(5) ![]()
Comparing this with Eq. (4) the term ![]() cancels out and we get
cancels out and we get
(6) ![]()
or
(7) ![]()
Thus in order for the trajectory to be special the ratio ![]() must be special:
must be special:
(8) 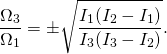
For our particular rigid body that we often use, with ![]() we should have
we should have
(9) ![]()
For our special trajectory that we were plotting in the last post Circles of eternal return
we had
(10) 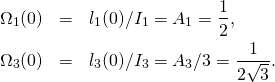
So it is just one particular way of satisfying Eq. (9). There are, however other ways. These other ways need to be researched.
We will do it in the next posts.




Thanks!
I like Musashi, I even forced myself to watch all the parts of loong looking-like-not-properly-ended movie about him with Toshiro Mifune (Yes, the first part is o.k, but try the rest..)