I did not know quaternions can manage the art of camouflage – until today. Camouflage and metamorphosis, they come together. People are wearing masks, to disguise, to cheat, to the extent that they cheat themselves. Quaternions took me by surprise. As a kid I was told about metamorphosis.
I never witnessed it myself. Until, as I said, today, until I looked at these two pictures:


In theory, if I am not making errors here, both images are supposed to represent the same story, except that it is being told by two different witnesses. It looks like a butterfly turning into caterpillar. How can it be? It is, after all, precise mathematics, not a psychology.
The first image represents the path in the group ![]() that we have discussed before in Introducing geodesics. Then, in Standing on the shoulders of giants – Reboot, examining the image obtained using my old code based on the paper of Van Zon and Schofield, I realized that:
that we have discussed before in Introducing geodesics. Then, in Standing on the shoulders of giants – Reboot, examining the image obtained using my old code based on the paper of Van Zon and Schofield, I realized that:
We have a nice curly trajectory, but there are also strange straight line spikes. On animation they are, perhaps, harmless. But if something like this happens with the software controlling the flight of airplanes, space rockets or satellites – people may die. There is a BUG in the algorithm.
Bugs are no good. As I have written it elsewhere:
I believe that the Universe has Purpose, that it is much like a computer program of great complexity, and that “we” – the IGUS-es – have a role in its evolution. For a while our role can be described simply as “debugging units.” In short, my present answer to the question “why are we here?” reads: DEBUGGING THE UNIVERSE.
With the somewhat less ambitious task of removing the zigzag bug from the spinning quaternion history we decided to follow the giants and we have ended in the new algorithm based on the paper and the code by Celledoni and Zanna, the code described in The final answer for the Universe in which m<1. I will repeat this code here, with a small change that makes it more universal, as discussed in Attitude matrix for m<1.
The solution
(1) 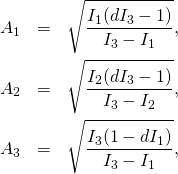
while for the other one, with ![]() we take
we take
(2) 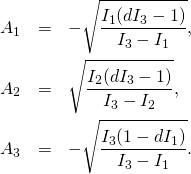
Let
(3) 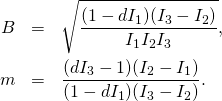
The solution ![]() of the Euler’s equations is given by
of the Euler’s equations is given by
(4) 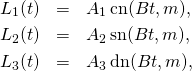
With constants ![]() and
and ![]() defined as
defined as
(5) 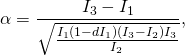
(6) ![]()
we set the phase variable ![]() as
as
(7) ![]()
where the Jacobi function ![]() is defined as
is defined as ![]()
Then the quaternionic attitude solution is given by ![]() with
with
(8) 
Why is this better than the previous formulas that were producing BUGS? The secret is in the denominator!
In the formulas for ![]() and
and ![]() we have
we have ![]() in the denominator. That is
in the denominator. That is ![]() The constant
The constant ![]()
is given by
![Rendered by QuickLaTeX.com \[A_1=\sqrt{\frac{I_1 (d I_3-1)}{I_3-I_1}}.\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-3a9c0f0b88eb7a45faccf4b1833b60b1_l3.png)
The smallest possible value of ![]() is
is ![]() then
then ![]() . The largest possible value of
. The largest possible value of ![]() while
while ![]() is
is ![]() when
when ![]() Then, with
Then, with ![]()
![]()
Therefore ![]() therefore
therefore ![]() (Remember that
(Remember that ![]() is a cosinus of the amplitude!). So, we never have a problem with the denominator! That is the advantage of the new algorithm! No infinities, all is finite, what a relieve!
is a cosinus of the amplitude!). So, we never have a problem with the denominator! That is the advantage of the new algorithm! No infinities, all is finite, what a relieve!
So, we take our flagship example with ![]() we choose
we choose ![]() just a little bit over the minimal value of
just a little bit over the minimal value of ![]() and we draw the stereographic projection of
and we draw the stereographic projection of ![]() from
from ![]() to
to ![]()
What we get is the second image.
No resemblance whatsoever to the first one.
And yet, they are supposed to represent the same reality! How can it be possible? They are like day and night …

So, I created the METAMORPHOSIS – a continuous group translation.

There is still something strange there…. And it needs to understood. Life is exciting.




larges ->
largest
“ is
is 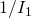 . Then
. Then  ,
,  . …”
. …”
For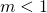 largest possible value of
largest possible value of 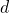 is
is 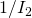 .
.
Am trying to fix. Thanks.
I’m lost. than
than 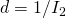
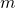 when
when 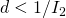 .
.
I know that if
but
I don’t know what is
But Eq. (3) gives you the formula for m ….
Ark,
correct me if I am wrong:
In the case of pendulum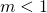 applied to high energies.
applied to high energies.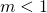 applies to low energies.
applies to low energies.
In the case of non-symmetric top
I think you are right. Somewhat strange …