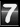We continue, from the previous post, with the beauty of the group SU(1,1). We already know that it looks like a doughnut, it feels like a doughnut, and it tastes like a doughnut. Yummy.

We represented SU(1,1) as a product of the open unit disk D and the circle parametrizing it by ![]() and
and ![]() . The circle group U(1) can be considered as a subgroup of SU(1,1). We analyzed orbits of the right action of U(1) on SU(1,1) using the (
. The circle group U(1) can be considered as a subgroup of SU(1,1). We analyzed orbits of the right action of U(1) on SU(1,1) using the (![]() parametrization:
parametrization:

The orbits are circles going around the doughnut. Every point of ![]() determines one orbit.
determines one orbit.
What about orbits of the left action? The truth is: we will not need them in what follows, but it is natural question to ask, so why not to ask?
So, let us take ![]() of the form
of the form
(1) ![]()
We take ![]() in SU(1,1), represent it as
in SU(1,1), represent it as ![]() , and we contemplate the product
, and we contemplate the product ![]() – with
– with ![]() fixed and
fixed and ![]() running from
running from ![]() to
to ![]() , we get one orbit. In order to represent the points of this orbit in terms of parameters
, we get one orbit. In order to represent the points of this orbit in terms of parameters ![]() and
and ![]() we need to represent
we need to represent ![]() as
as ![]() We do it by using a little trick, one of the standard tricks that every magician knows. We write
We do it by using a little trick, one of the standard tricks that every magician knows. We write
(2) ![]()
Here we used the fact that ![]() are unitary,
are unitary, ![]() and that they have the group property
and that they have the group property ![]() From the fact that
From the fact that ![]() are unitary follows even more.
are unitary follows even more. ![]() is Hermitian, therefore
is Hermitian, therefore ![]() is also Hermitian. Moreover,
is also Hermitian. Moreover, ![]() has the same eigenvalues as
has the same eigenvalues as ![]() Since
Since ![]() is positive, therefore
is positive, therefore ![]() is also positive, and it is also an an element of SU(1,1), therefore it must be of the form
is also positive, and it is also an an element of SU(1,1), therefore it must be of the form ![]() for some
for some ![]() . By direct calculation we find that
. By direct calculation we find that
(3) 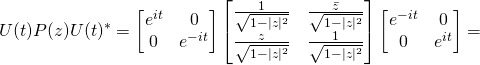
![Rendered by QuickLaTeX.com \[ =\begin{bmatrix}\frac{1}{\sqrt{1-|z|^2}}&\frac{e^{2it}\bar{z}}{\sqrt{1-|z|^2}}\\ \frac{e^{-2it}z}{\sqrt{1-|z|^2}}&\frac{1}{\sqrt{1-|z|^2}}.\end{bmatrix}\]](http://arkadiusz-jadczyk.eu/blog/wp-content/ql-cache/quicklatex.com-bc533a74aec856e9055cadcc4081b885_l3.png)
Now, since ![]() we deduce that
we deduce that ![]() Therefore the orbit is a path around the donut that, while going around, moves on a circle around the center of the disk – the cross-section of the donut. While going once around the donut, it makes two full circles in the disk – a closed spiral.
Therefore the orbit is a path around the donut that, while going around, moves on a circle around the center of the disk – the cross-section of the donut. While going once around the donut, it makes two full circles in the disk – a closed spiral.
The centers of the disks form a separate orbit. It is the orbit of both right and left action. The centers of the disks correspond to ![]()

So, we know the orbits of U(1) acting from the left. As I mentioned above, we will not need them. What we will need is the description of the left action of the group S(1,1) on the space of right circular orbits. This will be explained in the next post, and the kitty is already waiting