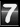Day: April 6, 2017

SU(1,1) preserves angles

Posted on by arkajad

In the last post, SU(1,1) straight lines on the disk, we have seen families of straight lines of the hyperbolic geometry on the disk. Here is another family:

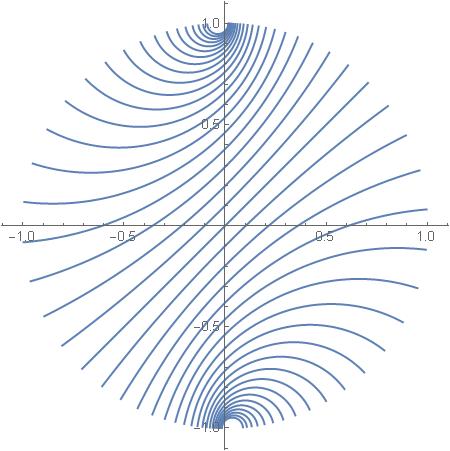
These lines are straight and they are parallel to each other, except that not in Euclidean geometry of the plane, but in the hyperbolic geometry that is based on constructions that are invariant with respect to SU(1,1) fractional linear transformations that we have met in previous notes.

These lines are obtained by applying SU(1,1) transformations to one straight line. Therefore they are not only all straight, but they all have the same length. This observation is not, however, very revealing, because, as we will see later, in the forthcoming notes, all these lines are of infinite length. The reason that they have infinite length is that they extend to the very ends of the disk universe.

In order to learn something about the length in the hyperbolic geometry of the disk let us take a segment of a straight line that is finite. I am taking the segment defined by y=0 and 1/2\leq x\leq 1/2. I apply to this segment transformations from the one-parameter group A_1(t) of SU(1,1) transformations defined in the previous post. Here is the result:

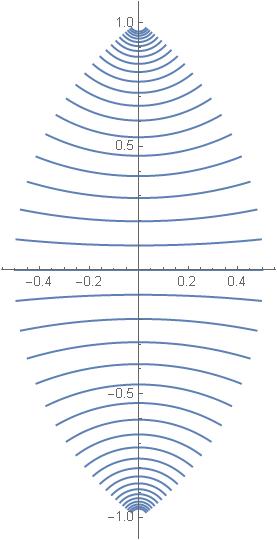
The right ends are on the trajectory of A_1(t) passing through the point (1/2,0). The one-parameter group A_1(t) leaves the vertical line invariant (even though it moves points on this line). Therefore the right ends are equidistant from the middle vertical straight line. But these points, even if they are in a constant distance from a straight line, are not on a straight line. This observation is related to the question asked by Bjab. In my reply I mentioned that straight lines of the hyperbolic geometry of the disk are segments of circles that meet the boundary at right angles. The pictures seem to support this property, but I did not give any proof of it, even a “baby proof”. It is now time to fill this hole.

We will show that transformations from SU(1,1) preserve angles. Of course they would certainly preserve “hyperbolic angles”, by definition of hyperbolic geometry, but here we will show that they preserve Euclidean angles. They do not preserve Euclidean lengths, but angles they do preserve! One says: they are conformal.

What would it mean that angles are preserved? Let us take a point z_0 and two curves \gamma_1(t), \gamma_2(t) such that \gamma_1(0)=\gamma_2(0)=z_0, that meet at some angle \alpha_0 at z_0. If A is a matrix in SU(1,1), it sends the point z_0 to a new point z_0', and it sends the curves \gamma_1 and \gamma_2 to \gamma_1' and \gamma_2'. The curves \gamma_1' and \gamma_2' meet at z_0' at some angle \alpha_0'. What we want to show is that \alpha_0'=\alpha_0.

First we are going to simplify our task by using what we already know.

We know that SU(1,1) acts on the disk transitively. We can always move the point z_0 to the origin z=0. If we are able to prove our statement for all SU(1,1) transformations and z_0=0, then it will immediately follow that the statement is true in general.

We know that every transformation from SU(1,1) can be decomposed into U(1) rotation U(\theta) and a positive matrix P(z). Rotations are just Euclidean rotations about the center of the disk. They evidently preserve Euclidean angles. It is therefore enough to consider P(z) transformations.

Let therefore \gamma_1(t), \gamma_2(t) be such that \gamma_1(0)=\gamma_2(0)=0. In coordinates \gamma_1(t) is described by functions z_1(t)=(x_1(t),y_1(t)),
while \gamma_2(t) is described by functions z_2(t)=(x_2(t),y_2(t)). Tangent vectors to \gamma_1 and \gamma_2 at z=0 have components \dot{\gamma}_1(0)=(\dot{x}_1(0),\dot{y}_1(0)) and \dot{\gamma}_2(0)=(\dot{x}_2(0),\dot{y}_2(0)) respectively. The angle \alpha_0 is determined by

    \[ \cos \alpha_0=\frac{\dot{\gamma}_1(0)\cdot\dot{\gamma}_2(0)}{|\dot{\gamma}_1(0)||\dot{\gamma}_2(0)|}.\]

Let us now take P(z), with z=x+iy

(1)   \begin{equation*} P(z)=\begin{bmatrix}\frac{1}{\sqrt{1-|z|^2}}&\frac{\bar{z}}{\sqrt{1-|z|^2}}\\ \frac{z}{\sqrt{1-|z|^2}}&\frac{1}{\sqrt{1-|z|^2}}\end{bmatrix}.\end{equation*}

It transforms z_1(t) into z_1'(t) given by

(2)   \begin{equation*}z_1'(t)=\frac{z_1(t)+z}{\bar{z}z_1(t)+1}.\end{equation*}

Now, we differentiate with respect to t at t=0 remembering that z_1(0)=0. We use the standard quotient rule,

even if here we apply it to a function with complex values. The result that I am getting is:

(3)   \begin{equation*}\dot{z}_1'(0)=(1-|z|^2)\dot{z}_1(0).\end{equation*}

Similarly we obtain

(4)   \begin{equation*}\dot{z}_2'(0)=(1-|z|^2)\dot{z}_2(0).\end{equation*}

Therefore the components of the transformed vectors are equal to the components of the original vectors multiplied by the same positive factor. It follows that the angles between them are the same.

Of course the proof above is a baby proof. Adults know that any holomorphic transformation preserves angles on the complex plane. Easy proof can be found here.