Day: April 12, 2017

Following Einstein: deriving Riemannian metric on the Poincaré disk

Posted on by arkajad

There is no geometry without metry. That is, without metric. It was Bernhard Riemann who gave the foundations to what we call today “Riemannian geometry”. When Einstein learned Rimennian geometry, he was able to compete with smart mathematicians and lay the foundations of the theory of gravitation – the General Relativity Theory.

“[In 1912] I suddenly realized that Gauss’s theory of surfaces holds the key for unlocking this mystery. I realized that Gauss’s surface coordinates had a profound significance. However, I did not know at that time that Riemann had studied the foundations of geometry in an even more profound way. I suddenly remembered that Gauss’s theory was contained in the geometry course given by Geiser when I was a student… I realized that the foundations of geometry have physical significance. My dear friend the mathematician Grossmann was there when I returned from Prague to Zürich. From him I learned for the first time about Ricci and later about Riemann. So I asked my friend whether my problem could be solved by Riemann’s theory [Pais’s italics], namely, whether the invariants of the line element could completely determine the quantities I had been looking for.”

Albert Einstein, as quoted by Abraham Pais in Subtle is the Lord, Pais’s scientific biography of Einstein.

So, it is time for us to get familiar with this “line element“. Here it is, written with the hand of Albert Einstein himself, probably in 1913, in his Zurich notebook:

From A Peek into Einstein’s Zurich Notebook“” by John D. Norton

We want to find our “line element” on the disk. Equivalently: we want to find the metric tensor G_{\mu\nu}.

That is, when from a point with disk coordinates (x,y) we make a small step, and arrive at the point with coordinates (x+dx,y+dy) what will be the length ds of this step? If the geometry were Euclidean, and our coordinates were Cartesian, rectangular, the answer would be simple: ds^2=dx^2+dy^2 from the Pythagoras formula. But our geometry is non-Euclidean. And we want our step length to be invariant under SU(1,1) transformations, which are non-linear on the disk. What to do?

We do what Einstein did in 1912

Einstein1912

We calculate. By the way: as we can learn from History of General Relativity and Gravitation, on his way to General Theory of Relativity Einstein was making errors

Two fundamental errors led Einstein to reject generally covariant gravitational field equations for over two years as he was developing his general theory of relativity. The first is now well known. It was the presumption that weak, static gravitational fields must be spatially flat and a corresponding assumption about his weak field equations. I conjecture that a second hitherto unrecognized error also defeated Einstein’s efforts: he unwittingly reified his spacetime coordinate systems. The same error, months later, allowed the hole argument to convince Einstein that all generally covariant gravitational field equations would be physically uninteresting.

While doing our calculations we will try to avoid errors, at least those computational. We will listen to Gottfried Leibniz who, as mentioned in the last note, has made this advice:

“It is unworthy of excellent men to lose hours like slaves in the labor of calculation which could be relegated to anyone else if machines were used.”

Again we will use a machine, though a different one than in From SU(1,1) to the Lorentz group.

As we have learned in From SU(1,1) to the Lorentz group, a point (x,y) on the disk determines a point (X,Y,T) on the hyperboloid in three-dimensional space-time

Space-time hyperboloid and the Poincare disk models

When we are making a small step (dx,dy) on the disk, we are making also a small step (dX,dY,dT) on the hyperboloid. Well, I am joking. When our step on the disk is very close to the boundary, the corresponding step on the hyperboloid can be “huge”. What I really mean is: when we make an infinitesimally small step …. The concept of an infinitesimally small step belongs to the calculus, and I will assume that we know how to use the elementary calculus concepts.

In the the previous post we used the formulas expressing (X,Y,T) as functions of (x,y):

(1)   \begin{eqnarray*} X&=&\frac{2x}{1-x^2-y^2},\\ Y&=&\frac{2y}{1-x^2-y^2},\\ T&=&\frac{1+x^2+y^2}{1-x^2-y^2}. \end{eqnarray*}

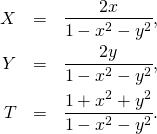
From these formulas we can calculate (dX,dY,dT) in terms of (dx,dy) according to the following general prescription

(2)   \begin{eqnarray*} dX&=&\frac{\partial X}{\partial x}dx+\frac{\partial X}{\partial y}dy,\\ dY&=&\frac{\partial Y}{\partial x}dx+\frac{\partial Y}{\partial y}dy,\\ dT&=&\frac{\partial T}{\partial x}dx+\frac{\partial T}{\partial y}dy. \end{eqnarray*}

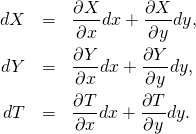
We can do these calculations by hand, but that would be unworthy of excellent men. Machine will do it for us. Once we know (dX,dY,dT) we can calculate the corresponding line element using the formula of special relativity, a generalization of the Pythagoras law from space to space-time. I our case it is now convenient to chose the signature (+1,+1,-1) then

(3)   \begin{equation*}ds^2=dX^2+dY^2-dT^2.\end{equation*}

I let Maxima to do the calculations using this code:

X(x,y):=2*x/(1-x^2-y^2);
Y(x,y):=2*y/(1-x^2-y^2);
T(x,y):=(1+x^2+y^2)/(1-x^2-y^2);
factor(ratsimp(
(diff(X(x,y),x)*dx+diff(X(x,y),y)*dy)^2+
(diff(Y(x,y),x)*dx+diff(Y(x,y),y)*dy)^2-
(diff(T(x,y),x)*dx+diff(T(x,y),y)*dy)^2);

If you want, save this code as a file, say, “ds2.mac”. Install and run wxMaxima, use File/Batch File … to load the code. The answer is produced immediately:

(4)   \begin{equation*}ds^2=\frac{4(dx^2+dy^2)}{(1-x^2-y^2)^2}.\end{equation*}

And that is the famous line element of hyperbolic geometry – see Metric and volume element on the Poincaré disk on Wikipedia.

We will yet have to find out what can we do with it? Lot of things. We can find geodesics (we have already guessed what they are), curvature …. Yes, our disk is curved even if it does not look so.