Day: April 13, 2017

Hyperbolic angels and demons

Posted on by arkajad

In SU(1,1) preserves angles we have seen this picture:

Fig. 1

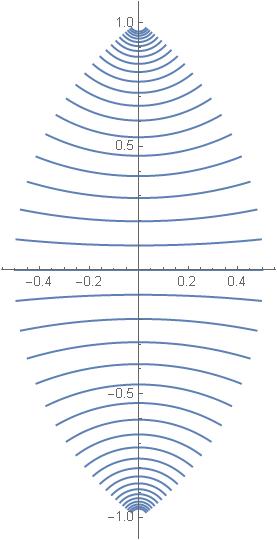
These are straight lines on the disk obtained from the interval [-0.5,0.5] on the real axis by the action of a one-parameter family A_1(t) of left shifts from SU(1,1). Since our geometry is, by definition, invariant under such transformations, all these lines are of equal length.

I thought it would be interesting to overlay these lines, obtained numerically, with Escher’s Angels and Demons picture to see how well Escher’s drawing corresponds to calculations. Here is the result:

Escher’s Angels and Demons and hyperbolic geometry

As far as I can see angels and demons do not know how to use computers. They work using intuition and aesthetic feelings. And yet Escher’s drawing corresponds to calculations almost perfectly.

In the last post, Following Einstein: deriving Riemannian metric on the Poincaré disk, \url{http://arkadiusz-jadczyk.eu/blog/2017/04/einstein-deriving-riemannian-metric-poincare-disk/} we have obtained the formula for the distance on the disk:

(1)   \begin{equation*}ds^2=\frac{4(dx^2+dy^2)}{(1-x^2-y^2)^2}.\end{equation*}

We can use it to find, say, the distance of a point (0,y_0) on the vertical axis from the origin. Tha path is paramatrized by (0,y) where y varies from 0 to y_0. Therefore the length of the path
is

    \[ s=\int_0^{y_0} ds= \int_0^{y_0} \frac{2 dy}{1-y^2}=2|\mathrm{arctanh} (y_0)|.\]

So, we have

(2)   \begin{equation*} s(y)=2|\mathrm{arctanh} (y)|.\end{equation*}

For producing Fig. 1 we used the family A_1(t) of SU(1,1) matrices;

    \[A_1(t)=\begin{bmatrix}\cosh(t)&i\sinh(t)\\-i\sinh(t)&\cosh(t).\end{bmatrix}\]

A_1(t) implements fractional linear transformation

    \[A_1(t):z\mapsto \frac{\cosh(t)z-i\sinh(t)}{i\sinh(t)z +\cosh(t)}.\]

Thus

(3)   \begin{equation*}A_1(t):0\mapsto z(t)=-i\tanh(t).\end{equation*}

The distance from the origin to z(t), along the vertical axis, is therefore

    \[s(t)=2|\mathrm{arctanh}(-\tanh(t))|=2|t|.\]

It follows that the parallel lines in Fig. 1 are all equidistant, if the distance between them is measured along the vertical axis.

That was our first use of the formula for the line element of the non-Euclidean hyperbolic geometry of the Poincaré disk. We will have to play with it a little bit more, so that we will not be afraid that it will bite us.