It is important to notice that the left action of SU(1,1) on itself maps right circular orbits of U(1) onto right circular orbits.

Abstractly it follows from the following reasoning:
Question: When are the given two points ![]() and
and ![]() in SU(1,1) on the same orbit of U(1) acting from the right?
in SU(1,1) on the same orbit of U(1) acting from the right?
Answer: It happens if and only if there exists ![]() in U(1) such that
in U(1) such that
![]()
Now suppose we move ![]() and
and ![]() into
into ![]() and
and ![]() by left translating with a given element
by left translating with a given element ![]() of SU(1,1):
of SU(1,1):
![]()
Are ![]() and
and ![]() on one orbit? That is: does there exist
on one orbit? That is: does there exist ![]() in U(1) such that
in U(1) such that ![]() ? And the answer is: YES. Even more, they are related by the same
? And the answer is: YES. Even more, they are related by the same ![]()
This follows from the fact that left and right actions of the group commute, which follows from the fact that group multiplication is associative:
![]()
So by acting from the left with a given element the circular orbit is transformed into another (perhaps the same) circular orbit. Circular orbits are parametrized by points ![]() of the unit disk
of the unit disk ![]() . Therefore SU(1,1) acts on the unit disk. That is abstract. But how it is in equations? The answer follows easily using the formula that we already know from previous posts about SU(1,1).
. Therefore SU(1,1) acts on the unit disk. That is abstract. But how it is in equations? The answer follows easily using the formula that we already know from previous posts about SU(1,1).
Suppose we are given ![]() with
with ![]() We construct from it a positive matrix
We construct from it a positive matrix ![]() in SU(1,1) using the prescription given in Eq. (8) from SU(1,1) decomposition:
in SU(1,1) using the prescription given in Eq. (8) from SU(1,1) decomposition:
(1) 
Now we act on it from the left with an element ![]() in SU(1,1):
in SU(1,1):
(2) ![]()
We obtain another element ![]() of SU(1,1)
of SU(1,1)
(3) ![]()
Therefore
(4) 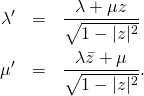
Now we calculate ![]() from Eq. (11) in SU(1,1) parametrization:
from Eq. (11) in SU(1,1) parametrization:
(5) ![]()
Thus we arrived at Eq. (15) from Getting hyperbolic. It was postulated there without any explanation. Now we have derived it.
Notice that ![]() maps the origin of the disk, the point
maps the origin of the disk, the point ![]() , into
, into ![]() Therefore
Therefore ![]() , for which
, for which ![]() and
and ![]() maps
maps ![]() into
into ![]()
It follows that the action of SU(1,1) on the disk ![]() is transitive. For any two points
is transitive. For any two points ![]() in
in ![]() there exist
there exist ![]() in SU(1,1) that transforms
in SU(1,1) that transforms ![]() into
into ![]() using the transformation (5). Namely, we know that
using the transformation (5). Namely, we know that ![]() transforms
transforms ![]() into
into ![]() , and
, and ![]() transforms
transforms ![]() into
into ![]() . Therefore
. Therefore ![]() transforms
transforms ![]() into
into ![]() . Another way of expressing the particular properties of this action is by saying that
. Another way of expressing the particular properties of this action is by saying that ![]() is a homogeneous space for SU(1,1), with
is a homogeneous space for SU(1,1), with ![]() as the stability group.
as the stability group.
Indeed, for the matrices from ![]() we have
we have ![]() therefore they map
therefore they map ![]() into
into ![]() Conversely, as it is really easy to see, any matrix from SU(1,1) that transforms
Conversely, as it is really easy to see, any matrix from SU(1,1) that transforms ![]() into
into ![]() must be one of the
must be one of the ![]() matrices.
matrices.
Once we know that, we can start studying the geometry of the disk.

We do have transitive transformation group, here acting on ![]() . That means we are ready for implementation of the Erlangen Program. Quoting from Wikipedia:
. That means we are ready for implementation of the Erlangen Program. Quoting from Wikipedia:
The Erlangen program is a method of characterizing geometries based on group theory and projective geometry. It was published by Felix Klein in 1872 as Vergleichende Betrachtungen über neuere geometrische Forschungen. It is named after the University Erlangen-Nürnberg, where Klein worked.
By 1872, non-Euclidean geometries had emerged, but without a way to determine their hierarchy and relationships. Klein’s method was fundamentally innovative in three ways:
Projective geometry was emphasized as the unifying frame for all other geometries considered by him. In particular, Euclidean geometry was more restrictive than affine geometry, which in turn is more restrictive than projective geometry.
Klein proposed that group theory, a branch of mathematics that uses algebraic methods to abstract the idea of symmetry, was the most useful way of organizing geometrical knowledge; at the time it had already been introduced into the theory of equations in the form of Galois theory.
Klein made much more explicit the idea that each geometrical language had its own, appropriate concepts, thus for example projective geometry rightly talked about conic sections, but not about circles or angles because those notions were not invariant under projective transformations (something familiar in geometrical perspective). The way the multiple languages of geometry then came back together could be explained by the way subgroups of a symmetry group related to each other.
Wikipedia mentions also (with a silly mistake that I have fixed below skipping the first four words):
The covering group ofSU(2,2) is isomorphic to the covering group of SO(4,2), which is the symmetry group of a 4D conformal Minkowski space and a 5D anti-de Sitter space and a complex four-dimensional twistor space.The Erlangen program can therefore still be considered fertile, in relation with dualities in physics.
We have SU(1,1) – the baby toy version of the adult S(2,2). We will be playing with this toy in the following posts.






“right circular orbits of SU(1) onto right circular orbits.”
SU(1) – what is it?
Fixed. Thanks!
adult S(2,2) -> adult SU(2,2)
For Klein/conformal geometry, I find your blog and your papers to be much more useful than Wikipedia. Wikipedia never quite comes out and says something like the adult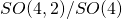 x
x 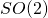 with 15-7=8 real or 4 complex dimensions or the toy
with 15-7=8 real or 4 complex dimensions or the toy 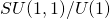 with 3-1=2 real or complex disk.
with 3-1=2 real or complex disk.
it form ->
it from
therefor ->
therefore
Do lambda prim and mu prim from (4) satisfy (2) ?
Thanks.
And yes, they do, by a somewhat tricky classical reasoning: every matrix from SU(1,1) satisfies (2). Matrices of SU(1,1) form a group. A and P(z) are in SU(1,1), therefore A’=AP(z) is in S(1,1). Therefore A’ is in SU(1,1), therefore A’satisfies (2).
Tricky is tricky.
But how can it be proved in lambdas and mus?
Tricky proof is ok, you can’t see an error, but nevertheless you would like to see the direct prof, using only the properties of complex numbers. Is that what you mean?
Yes
You tricked me. Fixed (4). Thank you!