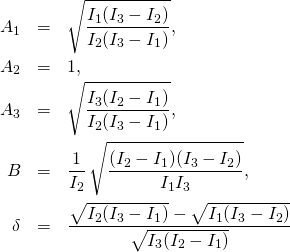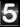According to the web site “How stuff works”
Our universe is devoid of perfect circles.
…
Only in the abstract world of pure mathematics can we find our perfect circle — a world of points and infinitely-thin lines with no room for particle inconsistencies or spherical oblateness.
…
In our world there is no true beauty, but we have an innate understanding and longing for the true form of beauty as it exists beyond the limits of our reality. There’s no true justice here, but we have a sense of it because the unreachable ideal exists in the realm of forms.
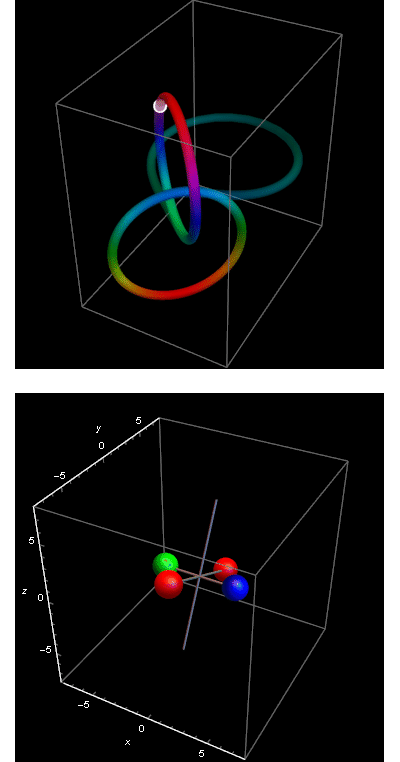
And this is what we are after: the true beauty. And nothing is going to stop us. Here it is. We stumbled upon it in our analysis of the internal mathematical structure of the Dzhanibekov effect. It is one of the simplest and at the same time one of the most amazing effects hidden in the laws of physics that were in principle known for centuries, but there is a difference between knowing and understanding.
In “Meetings with Remarkable Men” G. I. Gurdjieff wrote:
YES, PROFESSOR, KNOWLEDGE AND UNDERSTANDING ARE QUITE DIFFERENT. Only understanding can lead to being, whereas knowledge is but a passing presence in it. New knowledge displaces the old and the result is, as it were, a pouring from the empty into the void.
One must strive to understand; this alone can lead to our Lord God.
And in order to be able to understand the phenomena of nature, according and not according to law, proceeding around us, one must first of all consciously perceive and assimilate a mass of information concerning objective truth and the real events which took place on earth in the past; and secondly, one must bear in oneself all the results of all kinds of voluntary and involuntary experiencing.
Yes, we want to know, because knowledge protects (while ignorance endangers), but we also want to understand. For that math is needed. Here are, one more time, our remarkable circles, now rotating in front of you as in the Spring Fashion Show.

These are the two remarkable limit circles connected by the bridge.
And how do we get these limit circles?
Simple we go to the limits.
Recall the formulas from The mysterious paths on the three-sphere. Remember, we set ![]()
(1) 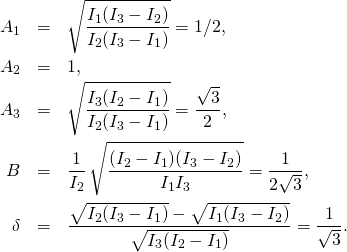
Define:
(2) 
where ![]()
Define
(3) ![]()
Define:
(4) 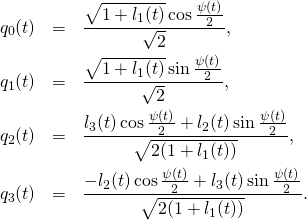
We want to know what happened in the distant path, and what will happen in the distant future. In other words we are interested in the asymptotic behavior at ![]() and
and ![]()
Let us start with ![]()

We see that in the past and in the future ![]() effectively vanishes. The same for
effectively vanishes. The same for ![]() For
For ![]() we have:
we have:
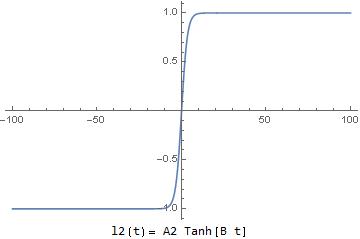
Therefore in the past, asymptotically, ![]() while in the future
while in the future ![]()
What about ![]() ?
?
Here is the plot of ![]()
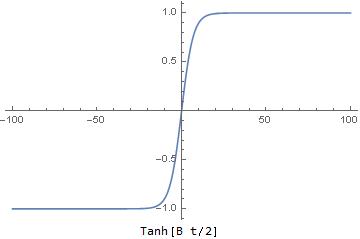
And ![]() Therefore asymptotically, in the past,
Therefore asymptotically, in the past,
(5) ![]()
(6) ![]()
Therefore asymptotically at ![]()
(7) ![]()
while for ![]()
(8) ![]()
where ![]() is given either by (5) or (6).
is given either by (5) or (6).
This will give us the two remarkable circles … In the next post. For now these circles should do: