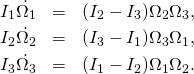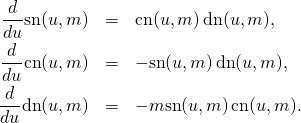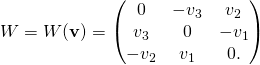Category: Euler’s equations

Crack in the Cosmic egg

Posted on by arkajad

From “The Crack in the Cosmic Egg: Challenging Constructs of Mind and Reality”, by Joseph Chilton Pearce (a must read!):

My neighbor was “seized and changed” somewhere in his final year of doctoral studies in topology. The structure of his mind, and his resulting world, were never again the same as that of non-mathematicians. He lived in a world of mathematical spaces. He loved to figure the spaces of knots, the kind you tie, though I could not relate his marvelous figurings to my shoelace world. He tried to show me, in beautifully-diagrammed hieroglyphics, how he could remove an egg from an intact shell through mathematical four-space. In my naive concreteness, frustrated that I had no ears to hear or eyes to see, I wanted him to apply his four-space miracle to a common hen’s egg. But my friend’s world was cerebral, his eggs those rare cosmic ones found in the inner land of thought, and his frustration at my blindness was as great as my own.
There is an eloquent madness in topology, but from that strange brotherhood’s abstractions lunar modules have been built. From their four-spaced absurdities have come real ships for spaces other than our own. The mythos leads the logos. The language of fantasy goes before the language of fact.

The physics and mathematics of asymmetric rigid top is harder than topology (see Asymmetric Spinning Top – The Hardest Concept To Grasp In Physics). It has its own egg’s tricks. A static egg has been critically analyzed in Racket about tennis racket. Then I started to move to the movies in The Flipping Top Movie that they will not show you in the movie theaters!.
“The mythos leads the logos.” But we did not yet finish with the mythos. So, let us contemplate these two animations produced by Mathematica software. Here they are:

And here is the code:

d = 0.501;
I1 = 1; I2 = 2; I3 = 3;
A1 = Sqrt[I1*(d*I3 – 1)/(I3 – I1)];
A2 = Sqrt[I2*(d*I3 – 1)/(I3 – I2)];
A3 = Sqrt[I3*(1 – d*I1)/(I3 – I1)];
B = Sqrt[(1 – d*I1)*(I3 – I2)/(I1*I2*I3)];
m = ((d*I3 – 1)*(I2 – I1))/((1 – d*I1)*(I3 – I2))
m1[t_] = A1*JacobiCN[B*t, m];
m2[t_] = A2*JacobiSN[B*t, m];
m3[t_] = A3*JacobiDN[B*t, m];
If[m < 1, tf = N[4*EllipticK[m]/B], tf = N[4*EllipticK[1/m]/(B*Sqrt[m])]];

g = x^2 + y^2 + z^2 – 1;
h = x^2/I1 + y^2/I2 + z^2/I3 – d;
cp = ContourPlot3D[{h == 0, g == 0}, {x, -1.5, 1.5}, {y, -1.5,
1.5}, {z, -1.8, 1.8},
MeshFunctions -> {Function[{x, y, z, f}, h – g]},
MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}},
ContourStyle ->
Directive[Orange, Opacity[0.5], Specularity[White, 30]],
PlotPoints -> 40, BoxRatios -> Automatic, Background -> Black,
Axes -> True,
AxesLabel -> {“\!\(\*SubscriptBox[\(L\), \(1\)]\)”,
“\!\(\*SubscriptBox[\(L\), \(2\)]\)”,
“\!\(\*SubscriptBox[\(L\), \(3\)]\)”}, AxesStyle -> White]

plot2b = Table[
Show[{cp,
Graphics3D[{Yellow,Sphere[{m1[a], m2[a], m3[a]}, 0.05]}]}], {a, -tf/2,
tf/2 – tf/10, tf/20}];
Export[“C:/egg0501.gif”, plot2b,
AnimationRepetitions -> Infinity, ImageSize -> {240, 240}]

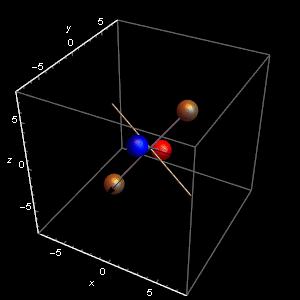
For the first animation the parameter $d$ is set to $d=0.499.$ What do we see? How is what we see in the animations related to the code? At the beginning of the code we see $I1 = 1; I2 = 2; I3 = 3;$ These are the characteristics of my olympic champion flipping and making vaults top. Girls do it their way

My rigid body does it even better. My rigid body has as its principal moments of inertia the first three prime numbers!. You can’t beat it! Of course there will be people that will attempt to discredit it, like: “Ït is using doping.” Which is not true at all! Or: “Number 1 is not a prime number”. They do not know history of mathematics. Read here from Wolfram MathWorld, Prime Number: “The number 1 is a special case which is considered neither prime nor composite (Wells 1986, p. 31). Although the number 1 used to be considered a prime (Goldbach 1742; Lehmer 1909, 1914; Hardy and Wright 1979, p. 11; Gardner 1984, pp. 86-87; Sloane and Plouffe 1995, p. 33; Hardy 1999, p. 46)…”. It is clear that it is the primest of all primes!

So, my spinning rigid body wins all competitions. Let me recall it explicitly from the previous post:

Now let us see these moments of inertia in a spectacular action of freely rotating in space. Not just rotating! Rotating and then flipping.

Click on the image to open the animation in a new window. Depending on your connection it may take a while. The size is almost 1 MB. You will see the flips. But why? What causes these flips?

The code above provides explicit solutions for the Euler’s equations for this champion. Look at the first animation. You see a white moving point. It moves along a curve in the northern hemisphere. It belongs to the family curves discussed in The Flipping Top Movie that they will not show you in the movie theaters!

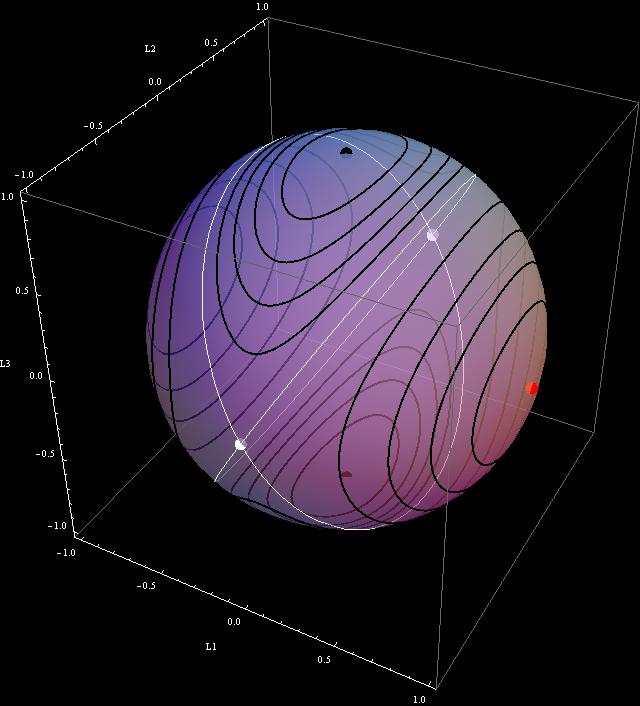
Except that the path on the animation is more elongated than on the image above. But why the northern hemisphere? Why not the southern one? It looks like racial discrimination!

Or the second animation. The yellow point moves only on path on the right. Not on the left. Why should leftist movements be neglected?

These are valid questions. Perhaps the Readers will try to answer them?

* Right now I am aware of the fact that this blog has two active readers.

Solving Euler’s equations

Posted on by arkajad

We are going to solve now Euler’s equations. In order to solve them in an intelligent way we need some preparation.

In “Angular momentum” we have derived Euler’s equations that govern rotations of a free rigid body about its center of mass:

(Euler)   \begin{eqnarray*}I_1\dot{\Omega_1}&=&(I_2-I_3)\Omega_2\Omega_3,\\ I_2\dot{\Omega_2}&=&(I_3-I_1)\Omega_3\Omega_1,\\ I_3\dot{\Omega_3}&=&(I_1-I_2)\Omega_1\Omega_2. \end{eqnarray*}

Here \Omega_1,\Omega_2,\Omega_3 are the components of the angular velocity vector in the body frame, while I_1,I_2,I_3 are the three principal moments of inertia.

Euler’s equations follow from conservation of the angular momentum vector with respect to space, as seen from the inertial laboratory frame. This is how we derived them in the previous post. The angular momentum vector in the laboratory frame is Q\mathbf{L}, where \mathbf{L} has components (I_1\Omega_1,I_2\Omega_2,I_3\Omega_3). Although we do not know Q (it needs to be found through solving differential equations), we know that it is an orthogonal matrix. And orthogonal matrix preserves the length of the vector. Since the components of the vector Q\mathbf{L} are constants, also its length is a constant. But the length of Q\mathbf{L} is the same as the length of \mathbf{L}, and the length squared L^2 of Q\mathbf{L} is

(1)   \begin{equation*} L^2=I_1^2\Omega_1^2+I_2^2\Omega_2^2+I_3^2\Omega_3^2.\end{equation*}

There is also another important constant of motion – kinetic energy. We denote by 2E the doubled kinetic energy:

(2)   \begin{equation*}2E=I_1\Omega_1^2+I_2\Omega_2^2+I_3\Omega_3^2.\end{equation*}

To see that indeed 2E is a constant of motion, we differentiate 2E with respect to t:

    \[\frac{d}{dt}\,2E=2(I_1\Omega_1\dot{\Omega_1}+I_2\Omega_2\dot{\Omega_2}+I_3\Omega_3\dot{\Omega_3}).\]

Now, we use the Euler’s equations and, surprise-surprise, everything on the right hand side cancels out:

(3)   \begin{multline*}\frac{d}{dt} 2E=2(I1\Omega_1(I_2-I_3)\Omega_2\Omega_3+\\ I_2\Omega_2(I_3-I_1)\Omega_1\Omega_3+\\ I_3\Omega_3(I_1-I_2)\Omega_1\Omega_2)=\\ 2(I_1I_2-I_1I_3+I_2I_3-I_2I_1+I_3I_1-I_3I_2)\Omega_1\Omega_2\Omega_3=0. \end{multline*}

Thus we get \frac{d}{dt}\,2E=0.

So, we have identified two important constants of motion. Whenever a rigid body rotates, it will change its orientation in space, its rotation axis may change its direction, but the absolute value L of the angular momentum given by Eq. (1) is constant in time. Kinetic energy is also constant in time. Yet these two constants are not completely independent. There are restrictions on the possible values of 2E if L^2 is given. To see this let us order I_1,I_2,I_3 so that

(4)   \begin{equation*}I_1\leq I_2\leq I_3.\end{equation*}

We then have:

    \[ I_12E=I_1(I_1\Omega_1^2+I_2\Omega_2^2+I_3\Omega_3^2)=I_1^2\Omega_1^2+I_1I_2\Omega_2^2+I_1I_3\Omega_3^2\leq L^2.\]

For the same reason we have

    \[ I_32E\geq L^2.\]

Let us introduce the constant d defined by

(5)   \begin{equation*}d=\frac{2E}{L^2}.\end{equation*}

Then we have

(6)   \begin{equation*}\frac{1}{I_3}\leq d\leq\frac{1}{I_1}.\end{equation*}

We can now move to solving the Euler’s equations (Euler) – at the top. To this end we compare them with the properties of the derivatives of Jacobi elliptic functions \sn,\cn,\dn that we have derived in “Derivatives of Jacobi elliptic am, sn, cn, dn“:

(7)   \begin{eqnarray*}\frac{d}{du}\mathrm{sn}(u,m)&=&\mathrm{cn}(u,m)\,\mathrm{dn}(u,m),\\ \frac{d}{du}\mathrm{cn}(u,m)&=&-\mathrm{sn}(u,m)\,\mathrm{dn}(u,m),\\ \frac{d}{du}\mathrm{dn}(u,m)&=&-m\mathrm{sn}(u,m)\,\mathrm{cn}(u,m).\end{eqnarray*}

According to our convention (4) on the right hand side of Euler’s equation we have signs (-,+,-). Our guess is that \Omega_2 is proportional to \sn. We do not know whether to assume \Omega_1 proportional to \cn or to \dn? Let us try \Omega_1 proportional \cn and \Omega_3 proportional to \dn. So, here is our “Ansatz”:

(8)   \begin{eqnarray*} \Omega_1(t)&=&A_1\cn(Bt,m),\\ \Omega_2(t)&=&A_2\sn(Bt,m),\\ \Omega_3(t)&=&A_3\dn(Bt,m).\\ \end{eqnarray*}

Question is: can we find A_1,A_2,A_3,B,m such that the Euler’s equation are satisfied automatically, given L and d?

The answer has been found long ago. We can see a solution in the 1894 book by Alfred Cardew Dixon, “The elementary properties of the elliptic functions” . But we want to do it in a modern way. Here, for instance, is REDUCE code that provides us with a solution:

%We derive a solution of Euler’s equations
o1(t):=A1*cn(B*t);
o2(t):=A2*sn(B*t);
o3(t):=A3*dn(B*t);
%To solve Euler’s equation we must have e1=e2=e3=0 where
e1:=(I1*DF(o1(t),t)-(I2-I3)*o2(t)*o3(t))/(dn(b*t)*sn(b*t));
e2:=(I2*DF(o2(t),t)-(I3-I1)*o3(t)*o1(t))/(cn(b*t)*dn(b*t));
e3:=(I3*DF(o3(t),t)-(I1-I2)*o1(t)*o2(t))/(sn(b*t)*cn(b*t));
% Here are properties of sn, cn, dn
For all v let DF(sn(v),v)=cn(v)*dn(v);
For all v let DF(cn(v),v)=-sn(v)*dn(v);
For all v let DF(dn(v),v)=-m*sn(v)*cn(v);
For all v let cn(v)**2=1-sn(v)**2;
For all v let dn(v)**2=1-m*sn(v)**2;
% en2 is twice kinetic energy:
en2:=I1*o1(t)^2+I2*o2(t)^2+I3*o3(t)^2;
% ll2 is square of angular momentum:
ll2:=I1^2*o1(t)^2+I2^2*o2(t)^2+I3^2*o3(t)^2;
OFF NAT;
OUT “H:\Reduce MyFiles\eu1.txt”;
e1;
e2;
e3;
% we use the three Euler’s equations in order to express A1,A2,A3 in terms of i1,i2,i3,b,m
xx:=solve({e1=0,e2=0,e3=0},{A1,A2,A3});
% We get four solutions, with different signs, we choose one with all signs plus:
PART(xx,3);
a1:= part(part(part(xx,3),1),2);
a2:= part(part(part(xx,3),2),2);
a3:= part(part(part(xx,3),3),2);
en2;
ll2;
% now we call angular momentum squared l^2 and we introduce d=en2/ll2.
% we then find m,b expressed through l and d
% again there are two solutions, with different signs. We choose both plus signs:
xxx:=solve({ll2=l^2,en2=l^2*d},{b,m});
b:=part(part(part(xxx,1),1),2);
m:=part(part(part(xxx,1),2),2);
% now we find final expressions for a1,a2,a3
a1:=a1;
a2:=a2;
a3:=a3;
SHUT “H:\Reduce MyFiles\eu1.txt”;
END;

The results spilled out by REDUCE are not yet nicely arranged. After the arrangement, taking into account our conventions, the answer takes the following form:

(9)   \begin{eqnarray*} A_1&=&L \sqrt{\frac{dI_3-1}{I_1(I_3-I_1)}},\\ A_2&=&L\sqrt{\frac{dI_3-1}{I_2(I_3-I_2)}},\\ A_3&=&L \sqrt{\frac{1-dI_1}{I_3(I_3-I_1)}},\\ B&=&L\sqrt{\frac{(1-dI_1)(I_3-I_2)}{I_1I_2I_3}},\\ m&=&\frac{(dI_3-1)(I_2-I_1)}{(1-dI_1)(I_3-I_2)}. \end{eqnarray*}

Now I should verify that it is indeed a solution. I was trying to do it using REDUCE, but I did not succeed. So, I will return to this problem in my next post (and I will also try to fix typos in this post). Hopefully I will be able to find a way of verifying for sure the above statements.

Update: The following REDUCE code verifies the solution on random data. On output it spits out three zeros.:
a1:=l*sqrt((d*i3-1)/(i1*(i3-i1)));
a2:=l*sqrt((d*i3-1)/(I2*(i3-i2)));
a3:=l*sqrt((1-d*i1)/(i3*(i3-i1)));
b:=l*sqrt((1-d*i1)*(I3-i2)/(i1*i2*i3));
m:=(d*i3-1)*(i2-i1)/((1-d*i1)*(i3-i2));
o1(t):=A1*cn(B*t);
o2(t):=A2*sn(B*t);
o3(t):=A3*dn(B*t);
For all v let DF(sn(v),v)=cn(v)*dn(v);
For all v let DF(cn(v),v)=-sn(v)*dn(v);
For all v let DF(dn(v),v)=-m*sn(v)*cn(v);
For all v let cn(v)**2=1-sn(v)**2;
For all v let dn(v)**2=1-m*sn(v)**2;
e1:=(I1*DF(o1(t),t)-(I2-I3)*o2(t)*o3(t))/(dn(b*t)*sn(b*t));
e2:=(I2*DF(o2(t),t)-(I3-I1)*o3(t)*o1(t))/(cn(b*t)*dn(b*t));
e3:=(I3*DF(o3(t),t)-(I1-I2)*o1(t)*o2(t))/(sn(b*t)*cn(b*t));
for all a,b let sqrt(a)*sqrt(b)=sqrt(a*b);
off rounded;
i1:=random(1000)/1000;
i2:=1.0+random(1000)/1000;
i3:=2.0+random(1000)/1000;
l:=random(10)/2;
d:=1/i3+(1/i1-1/i3)/2;

OFF NAT;
OUT “H:\Reduce MyFiles\eu3.txt”;
e1:=e1;
e2:=e2;
e3:=e3;
SHUT “H:\Reduce MyFiles\eu3.txt”;
END;

Update 2:

Both REDUCE and Mathematica are able to do the task in a symbolic mode, but not without human help. These programs have very smart simplification algorithms, but sometimes our eye see that two expressions are the same, though they have different forms, while the programs do not want to see it. Then we need to help the program. For instance with Mathematica, it did not want to see that a particular expression is zero, but it recognized that its square is zero! Like here:


Here is the Mathematica notebook verifying Euler’s equations.
So, I consider that the job is done, and that we do have a solution of Euler’s equations.

Angular momentum

Posted on by arkajad

Let me start with recalling from Dzhanibekov effect – Part 4: The equations of motion.
We consider a free rigid body, observed from a laboratory that is an inertial reference system. The body is rotating with a fixed point at the center of its mass. The center of mass is at rest with respect to the laboratory.

Let \mathbf{E}_1(t), \mathbf{E}_2(t), \mathbf{E}_3(t) be an orthonormal frame corotating with the body, and aligned with its principal axes, and let \mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3 be an inertial laboratory frame, both centered at the center of mass of the body. The two frames are related by time-dependent orthogonal matrix A(t)

\mathbf{E}_i=A_{ji}\mathbf{e}_j,\quad X_i= A_{ij}x_j.

The inverse of A is denoted by Q

Q= A^{-1}=A^t,

and it is often called the attitude matrix. For a rotating body, if X_i are coordinates of a fixed point in the body, then its coordinates in the laboratory system change in time:
{\bf x}(t)=Q(t){\bf X}.

Differentiating we get

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}{\bf X}=\frac{dQ}{dt}Q^{-1}(t)\,{\bf x}(t).

The matrix Q(t) is orthogonal, Q(t)Q(t)^t=I, therefore, by differentiating, the matrix \frac{dQ(t)}{dt}Q(t)^{-1} is antisymmetric. Every antisymmetric 3\times 3 matrix W can be written as

W = W({\bf v})=\begin{pmatrix}0& -v_3&v_2\\v_3&0&-v_1\\-v_2&v_1&0.\end{pmatrix}

Writing \frac{dQ(t)}{dt}Q(t)^{-1}$ as $W(\boldsymbol{\omega}(t)):

(*)   \[ \frac{dQ(t)}{dt}Q(t)^{-1}=W(\boldsymbol{\omega}(t)),\]

we find that

\frac{d{\bf x}(t)}{dt}=\frac{dQ(t)}{dt}Q(t)^{-1}{\bf x}(t)=\boldsymbol{\omega}(t)\times{\bf x}(t).

Acting with the matrix W(\omega) is equivalent to taking the crossproduct with vector \omega.

The vector \boldsymbol{\omega}(t) is the angular velocity vector in the laboratory frame.

We denote by \boldsymbol{\Omega} the body representative of the angular velocity vector \boldsymbol{\omega}, where we skip the time dependence, with components \Omega_1,\Omega_2,\Omega_3.
Thus

\boldsymbol{\omega}= Q \boldsymbol{\Omega},

(**)   \begin{equation*} W(\boldsymbol{\omega})=QW(\boldsymbol{\Omega})Q^t.\end{equation*}

In a comment to this post Bjab asked: why (**)? Where is it coming from?
Good question. We have the relation

    \[W(\Omega)\mathbf{v}=\Omega\times\mathbf{v}\]

for any vectors \Omega and \mathbf{v}. If Q is a rotation matrix with determinant 1, then it follows from the definition of the cross product (see e.g. Rotational invariance of cross product) that

    \[ Q\Omega\times Q\mathbf{v}=Q(\Omega\times\mathbf{v}). \]

Therefore

    \[W(Q\Omega)Q\mathbf{v}=QW(\Omega)\mathbf{v}.\]

Let us set Q\mathbf{v}=\mathbf{w},\, \mathbf{v}=Q^t\mathbf{v}. then

    \[W(Q\Omega)\mathbf{w}=QW(\Omega)Q^t\mathbf{w}.\]

Since \mathbf{w} can be arbitrary, we get

    \[W(Q\Omega)=QW(\Omega)Q^t.\]

Now, from Eq. (*)

(1)   \begin{equation*} W(\boldsymbol{\Omega})=Q^t\dot{Q},\end{equation*}

where \dot{Q}=dQ(t)/dt. In the body frame the inertia tensor I is diagonal I=\mathrm{diag}(I_1,I_2,I_3). The angular momentum vector \mathbf{L} in the body frame is then given by the formula

\mathbf{L}=I\boldsymbol{\Omega},
or

    \[L_1=I_1\Omega_1,\,L_2=I_2\Omega_2,\,L_3=I_3\Omega_3.\]

The definition of the angular momentum \mathbf{L} is thus similar to the definition of the linear momentum. Liner momentum \mathbf{p} is the product of mass m and velocity \mathbf{v}. Angular momentum, in the body frame, \mathbf{L} is a vector whose components are products of moments of inertia I_i and angular velocity components \omega_i. The expression for the angular momentum in the body frame is very simple, but the law of conservation of the angular momentum refers to angular momentum vector in the laboratory frame. The transition from the body to the laboratory frame is implemented by the attitude matrix Q. Therefore what is conserved is Q\mathbf{L}:

(2)   \begin{equation*}\frac{d}{dt} \left(Q(t)\mathbf{L}(t)\right)=0.\end{equation*}

From this we get:

    \[ \dot{Q}(t)\mathbf{L}(t)+Q(t)\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2}\]

From Eq. (1) we have that \dot{Q}=QW(\boldsymbol{\Omega}), therefore Eq. (??) reduces to

    \[ Q(t)W(\boldsymbol{\Omega})\mathbf{L}(t)+Q(t)\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2a}\]

or, multiplying by Q(t)^{-1} from the left:

    \[ W(\boldsymbol{\Omega})\mathbf{L}(t)+\frac{d}{dt}\mathbf{L}(t)=0.\label{eq:c2a}.\]

But W(\boldsymbol{\Omega})\mathbf{L}=\boldsymbol{\Omega}\times\mathbf{L}=-\mathbf{L}\times\boldsymbol{\Omega},
therefore

    \[ \frac{d}{dt}\mathbf{L}(t)=\mathbf{L}\times\boldsymbol{\Omega}.\label{eq:c2b}.\]

Using the definition \mathbf{L}=(I_1\Omega_1,I_2\Omega_2,I_3\Omega_3), we arrive at

(Euler)   \begin{eqnarray*}I_1\dot{\Omega_1}&=&I_2\Omega_2\Omega_3-I_3\Omega_3\Omega_2=(I_2-I_3)\Omega_2\Omega_3,\\ I_2\dot{\Omega_2}&=&I_3\Omega_3\Omega_1-I_1\Omega_1\Omega_3=(I_3-I_1)\Omega_3\Omega_1,\\ I_3\dot{\Omega_3}&=&I_1\Omega_1\Omega_2-I_2\Omega_2\Omega_1=(I_1-I_2)\Omega_1\Omega_2. \end{eqnarray*}

These are the famous Euler’s equations. At the end of Dzhanibekov effect – Part 4: The equations of motion they were written in terms of (L_1,L_2,L_3), Here they are written in terms of \Omega_1,\Omega_2,\Omega_3.

We need to solve them. But first we will look at them with a magnifying glass. In the next couple of posts.