Yesterday, while thinking about Dzhanibekov effect, gyroscopes and elliptic functions, I checked my mailbox and read the following email from one of the readers:
Dear Ark,
Can you write about Kozyriev mirrors in your future posts? Rossiya 1 did a documentary awhile ago still available here:
Kozyrev Mirrors_Breakthrough into the Future – (english subtitles)
What are your thoughts of what might be going on in these experiments? Do the Kozyriev mirror experiments have to do with time traveling and accessing the information field? Why a “concave” mirror or cylinder? What is special about this shape and the materials used? Would it be detrimental for people to experiment with these mirrors? Any scientific or informal thoughts on this subject will be most welcomed.
The truth is: in my imagination gyroscopes and Kozyrev’s mirrors are completely different subjects. But then I asked myself: or aren’t they?
After small search I have downloaded from the Internet THE SCIENCE OF TORSION, GYROSCOPES AND PROPULSION. It starts with
“SOMETHING IS MISSING IN THE SCIENCE OF SPINNING SYSTEMS”
My critical article on Shipov’s “4D gyroscopes” is mentioned there, but the works and ideas of Kozyrev are also mentioned.
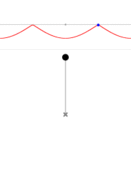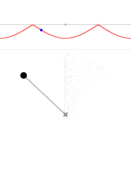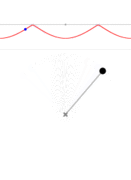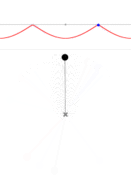
Wikipedia article on Kozyrev with his mirrors quotes “Akimov, A.E., Shipov, G. I., Torsion fields and their experimental manifestations, 1996” – the subject closely related to the “unconventional physics” of spinning objects. So, perhaps at some deeper level the two subjects are closely related? With this in mind I will have to read what is available about research done with Kozyrev’s mirrors. At present I know next to nothing, and what I once knew I have mostly forgotten. But I will keep it in mind, study, and in the future return the strange properties of space, vacuum, structured aether and Kozyrev mirrors. For now, however, I need to finish what I have started – nonlinear mathematical pendulum. Today we will discuss the expressions for its period.
Pendulum period: ![]()
In the previous post Rescaled Jacobi amplitude – general solution for the mathematical pendulum, we have derived a general formula for time evolution of a nonlinear mathematical pendulum
(1) ![]()
where ![]() is the ratio
is the ratio ![]() of maximal potential energy to maximal kinetic energy, and
of maximal potential energy to maximal kinetic energy, and ![]() where
where ![]() is the gravitational acceleration, and
is the gravitational acceleration, and ![]() is the length of the pendulum.
is the length of the pendulum.
The inequality ![]() means that the pendulum has sufficient kinetic energy to swing full circles. Lets us recall the graph of the amplitude function
means that the pendulum has sufficient kinetic energy to swing full circles. Lets us recall the graph of the amplitude function ![]()
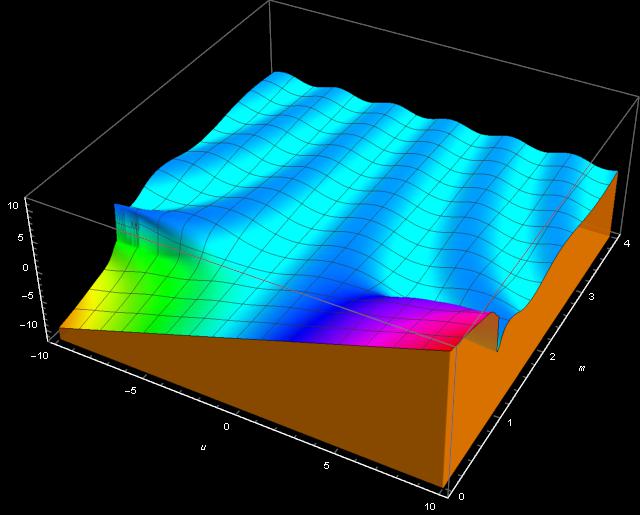
For ![]() the value of
the value of ![]() grows from left to right. That is clear: the angle
grows from left to right. That is clear: the angle ![]() constantly increases. But when it riches
constantly increases. But when it riches ![]() the pendulum, in fact makes a full circle. Therefore the period
the pendulum, in fact makes a full circle. Therefore the period ![]() of our pendulum is calculated from the formula
of our pendulum is calculated from the formula
(2) ![]()
We recall from Jacobi amplitude- realism or cubism that ![]() is the inverse function of
is the inverse function of ![]() the incomplete elliptic integral of the first kind given by (see also Wikipedia: Elliptic integral)
the incomplete elliptic integral of the first kind given by (see also Wikipedia: Elliptic integral)
(3) ![]()
Therefore Eq. (2) is equivalent to
![]()
The function under integral in Eq. (3) has the symmetry property that tells us that ![]() The value
The value ![]() is usually given the name: the complete elliptic integral of the first kind, and it is often denoted with the capital letter
is usually given the name: the complete elliptic integral of the first kind, and it is often denoted with the capital letter ![]() Thus we obtain:
Thus we obtain:
(4) ![]()
The case of ![]() is uninteresting, as it means either the pendulum of zero potential, or of infinite kinetic energy. In the case of
is uninteresting, as it means either the pendulum of zero potential, or of infinite kinetic energy. In the case of ![]() we have, in fact, two possible solutions. One is with
we have, in fact, two possible solutions. One is with ![]() constant,
constant, ![]() That is very unstable, like a pencil that stands on its tip. There is also second solution, one given by our formula with
That is very unstable, like a pencil that stands on its tip. There is also second solution, one given by our formula with ![]() The motion is non-periodic, there is just one flip all around the circle, and it takes infinite time.
The motion is non-periodic, there is just one flip all around the circle, and it takes infinite time.
Pendulum period: ![]()
For ![]() we have to return to the definition of the amplitude function – Eqs (1),(2) in Jacobi elliptic cn and dn:
we have to return to the definition of the amplitude function – Eqs (1),(2) in Jacobi elliptic cn and dn:
(5) ![]()
We can see from the graph above that for ![]() the function
the function ![]() oscillates periodically. Since, taking into account simplification of multiplying and dividing by
oscillates periodically. Since, taking into account simplification of multiplying and dividing by ![]() , we get
, we get
![]()
it follows that the period ![]() of
of ![]() is the same as the period of the function
is the same as the period of the function ![]() and it is the same as the period of the function
and it is the same as the period of the function ![]()
It is therefore given by the formula
![]()
therefore
For very small oscillation (very small kinetic energies) ![]() is very large and
is very large and ![]() is close to zero. The integrand in the definition of
is close to zero. The integrand in the definition of ![]() can be replaced by the constant
can be replaced by the constant ![]() , so that, for very large
, so that, for very large ![]() ,
, ![]() Therefore
Therefore ![]() can be replaced by
can be replaced by ![]() and Eq. (6) reduces to
and Eq. (6) reduces to
(7) ![]()
This is the standard formula for the linear pendulum with small oscillation. It was known to Galileo.