We start with a partial recall of events as they transpired so far. A month ago we became hyperbolic. The post Getting hyperbolic started with this sentence:
Without knowing it, during the last three posts (Our first field expedition, Our second field expedition, The Third Expedition) we became hyperbolic. Hyperbolic and conformal. Conformal and relativistic, relativistic and non-Euclidean.
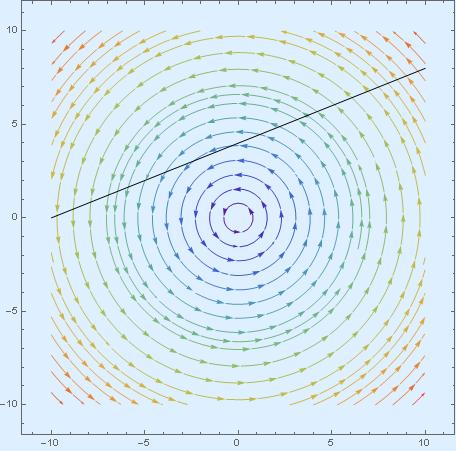
Then we introduced the group SU(1,1) and its action on the disk. Then, in From SU(1,1) to the Lorentz group we realized that the disk can be considered as a projection of a hyperboloid in 2+1 dimensional space-time, where the hyperboloid is inside the future light cone. We were contemplating the image below

and we have shown that there is a group homomorphism from SU(1,1) to the Lorentz group SO(2,1) of 2+1 dimensional special relativity. We have calculated the formula explicitly in Eq. (7) there. If ![]() is a complex matrix from SU(1,1) with
is a complex matrix from SU(1,1) with ![]() split into real and imaginary parts, then the real
split into real and imaginary parts, then the real ![]() matrix
matrix ![]() from SO(2,1) is given by the formula:
from SO(2,1) is given by the formula:
(1) 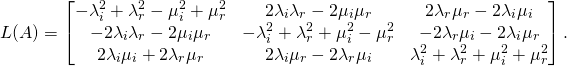
The map ![]() is a group homomorphism, that is
is a group homomorphism, that is ![]() and
and ![]() ( Of course in
( Of course in ![]() we denote by the same symbol
we denote by the same symbol ![]() identity matrices of different sizes.)
identity matrices of different sizes.)
After that, in Getting real, we used Cayley transform that defines group isomorphism between the complex matrix group SU(1,1) and the real matrix group SL(2,R). With
(2) ![]()
(3) ![]()
we have that if ![]() is a real matrix from SL(2,R) (i.e.
is a real matrix from SL(2,R) (i.e. ![]() ), then
), then ![]() is in SU(1,1). If we calculate explicitly
is in SU(1,1). If we calculate explicitly ![]() and
and ![]() in terms of
in terms of ![]() the result is:
the result is:
(4) 
Combining it with ![]() we obtain group homomorphism from SL(2,R) to SO(2,1). Explicitly
we obtain group homomorphism from SL(2,R) to SO(2,1). Explicitly
(5) 
So far, so good, but now there comes real magic!

We do not have to travel around the world, through SU(1,1) and hyperboloids. We will derive the last formula directly using a method that is similar to the one we used when deriving the map from quaternions to rotation matrices in Putting a spin on mistakes.
The Lie algebra sl(2,R) of the Lie group SL(2,R) consists of real ![]() matrices of zero trace – we call them “generators”. We already met three particular generators
matrices of zero trace – we call them “generators”. We already met three particular generators ![]() , for instance in SL(2,R) generators and vector fields on the half-plane, and I will skip this time primes as they have been denoted previously
, for instance in SL(2,R) generators and vector fields on the half-plane, and I will skip this time primes as they have been denoted previously
(6) 
Every element of sl(2,R) is a real linear combination of these three. So, ![]() can be considered as a basis of sl(2,R). For instance in SL(2,R) generators and vector fields on the half-plane we constructed a particular generator
can be considered as a basis of sl(2,R). For instance in SL(2,R) generators and vector fields on the half-plane we constructed a particular generator ![]() and
and ![]() defined as
defined as
(7) 
The Lie algebra sl(2,R) is a three-dimensional real vector space. But it is more than just a vector space. The group SL(2,R) acts on this space by what is called “the adjoint representation”. This is true for the Lie algebra of any Lie group. Here we have a particular case. Namely, if ![]() is in sl(2,R), that is if
is in sl(2,R), that is if ![]() has trace zero, and if
has trace zero, and if ![]() is in SL(2,R), that is the determinant of
is in SL(2,R), that is the determinant of ![]() is one, then
is one, then ![]() is also of zero trace (we do not need the property of determinant one for this). The map
is also of zero trace (we do not need the property of determinant one for this). The map ![]() is a linear map. Thus we have action, let us call it
is a linear map. Thus we have action, let us call it ![]() , of SL(2,R) on sl(2,R):
, of SL(2,R) on sl(2,R):
(8) ![]()
Remark: I will now be skipping primes that I was using to distinguish matrices from SL(2,R) from matrices from SU(1,1).
Evidently (from associativity of matrix multiplication) we have
![]()
Usually instead of ![]() one writes
one writes ![]() and uses the term “adjoint representation”. In short: the group acts on its Lie algebra by similarity transformations. Similarity transformation of a generator is another generators. Even more, by expanding exponential into power series we can easily find that
and uses the term “adjoint representation”. In short: the group acts on its Lie algebra by similarity transformations. Similarity transformation of a generator is another generators. Even more, by expanding exponential into power series we can easily find that
(9) ![]()
So sl(2,R) is a three dimensional real vector space and SL(2,R) acts on it by linear transformations.
But that is not all. In sl(2,R) we can define a very nice scalar product ![]() as follows
as follows
(10) ![]()
where ![]() is the trace of the product of matrices
is the trace of the product of matrices ![]() and
and ![]()
Why is this scalar product “nice”? What is so nice about it? It is nice, because with this scalar product the transformations ![]() are all isometries – they preserve this scalar product:
are all isometries – they preserve this scalar product:
(11) ![]()
The derivation of this last property follows from the definitions and from the property that similarity transformations do not change the trace.
So sl(2,R) is a three dimensional real vector space with a scalar product. But in sl(2,R) we have our basis ![]() It is easy to calculate scalar products of the basis vectors. We get the following matrix for the matrix
It is easy to calculate scalar products of the basis vectors. We get the following matrix for the matrix ![]() with entries
with entries
(12) ![]()
(13) 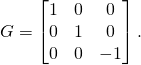
Thus sl(2,R) has all the properties of the Minkowski space with two space and one time dimensions. The generator ![]() has “time direction”, while
has “time direction”, while ![]() are “space directions”.
are “space directions”.
Once we have a basis there, we can calculate the components of the transformations ![]() in this basis:
in this basis:
(14) 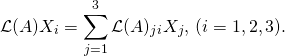
I used Mathematica to calculate ![]() for
for ![]() . Here is the result:
. Here is the result:
(15) 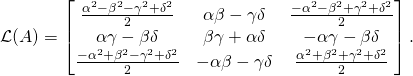
Here I admit that in this last formula I did copy and paste from Eq. (5) above. Because indeed that is what happened in the calculation – the result came identical. And that is the real magic. We do not need external space-time and hyperboloids. Everything is already contained in the group itself and in its Lie algebra!