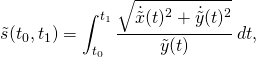We continue Becoming anti de Sitter.
Every matrix ![]() in the Lie algebra o(2,2) generates one-parameter group
in the Lie algebra o(2,2) generates one-parameter group ![]() of linear transformations of
of linear transformations of ![]() Vectors tangent to orbits of this group form a vector field. Let us find the formula for the vector field generated by
Vectors tangent to orbits of this group form a vector field. Let us find the formula for the vector field generated by ![]() The orbit through
The orbit through ![]() is
is
(1) ![]()
Differentiating at ![]() we find the vector field
we find the vector field ![]()
(2) ![]()
If ![]() is a matrix with components
is a matrix with components ![]() then
then ![]() has components
has components
(3) ![]()
Vectors tangent to coordinate lines are often denoted as ![]() . Therefore we can write the last formula as:
. Therefore we can write the last formula as:
(4) ![]()
In the last post Becoming anti de Sitter we have constructed six generators ![]() Their vector fields now become
Their vector fields now become
(5) ![]()
(6) ![]()
Bengtsson and Sandin in their paper “Anti de Sitter space, squashed and stretched” discussed in the previous note use coordinates ![]() . Our vector field
. Our vector field ![]() is the same as their
is the same as their ![]() , our
, our ![]() is the same as their
is the same as their ![]() etc.
etc.
In SL(2,R) Killing vector fields in coordinates we introduced six Killing vector fields acting on the group manifold SL(2,R). How they relate to the above six generators of the group O(2,2)?
Vectors from the fields ![]() are tangent to SL(2,R). We have expressed them in coordinates of the group SL(2,R)
are tangent to SL(2,R). We have expressed them in coordinates of the group SL(2,R) ![]() The manifold of SL(2,R) is a hipersurface of dimension 3 in
The manifold of SL(2,R) is a hipersurface of dimension 3 in ![]() endowed with coordinates
endowed with coordinates ![]() . What is the relation between components of the same vector in different coordinate systems? The formula is easy to derive and is very simple. If
. What is the relation between components of the same vector in different coordinate systems? The formula is easy to derive and is very simple. If ![]() are coordinates of the vector in SL(2,R) and
are coordinates of the vector in SL(2,R) and ![]() are coordinates of the same vector in
are coordinates of the same vector in ![]() then
then
(7) ![]()
How ![]() depend on
depend on ![]() ? That is simple. In SL(2,R) vector fields in coordinates we have represented each matrix
? That is simple. In SL(2,R) vector fields in coordinates we have represented each matrix ![]() from SL(2,R) as
from SL(2,R) as
(8) 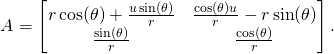
On the other hand, Becoming Anti-de Sitter, we represented it as
(9) ![]()
Therefore coordinates ![]() are easily expressed in terms of
are easily expressed in terms of ![]() . It remains to do the calculations. I have used computer algebra software to make these calculations for me. My Mathematica notebook doing all calculations can be downloaded from here. The result of all these calculations is the expression of vector fields
. It remains to do the calculations. I have used computer algebra software to make these calculations for me. My Mathematica notebook doing all calculations can be downloaded from here. The result of all these calculations is the expression of vector fields ![]() in terms of the generators of O(2,2) used in the paper on anti de Sitter spaces. Here is what I have obtained:
in terms of the generators of O(2,2) used in the paper on anti de Sitter spaces. Here is what I have obtained:
(10) 
Bengtsson and Sandin introduce then their own parametrization of SL(2,R) and study the invariant metric on the group. We will find the connection between ours and their approaches in the next posts. We came to our problems starting from T-handles spinning freely in zero gravity. They are studying spinning black holes. It is interesting to see and to research similarities.