First about Kozyrev’s mirrors. I have started to study the subject. That is a real adventure in a real jungle! First of all it seems they are not “Kozyrev’s”. They have been invented and investigated by V. P. Kaznacheev, but Kaznacheev was very much impressed by Kozyrev’s work, so he decided to call the mirrors with Kozyrev’s name. The work, as I understand, have started in Novosibirsk under the guidance of Kaznacheev for many years. It is now being continued at the “International Scientific Research Institute of Cosmoplanetary Anrthropoecology“. The web site of the institute is all in Russian, but the publication page of the “institute” has some English text. In particular you can find there these links:
http://www.altaibooks.com/trofimov2016.pdf
http://www.altaibooks.com/trofimov2012.pdf
These are interviews in English with A. Trofimov, who was a collaborator of Kaznacheev, and now is the head of the Institute. Here are some excerpts form the 2016 interview, so that you can form an idea about what kind of research is being conducted in Novosibirsk now.
We humans tend to think the way to wisdom is by looking outwards, but it’s not. We already have wisdom. We need only to look inward. Dr. Alexander Trofimov, Director of the Institute for Scientific Research in Cosmoplanetary Anthropoecology (ISRICA) in Novosibirsk, Russia, has spent a lifetime honing his skills at looking inward.
….
Now, he tells me, he and his team of inner-space cosmonauts have another breakthrough—they have begun actual communication with extraterrestrials.
….
At ISRICA, at our New International Center of Kozyrev’s Space Investigations we are pursuing correct scientific accompaniment of these contacts. We are open for cooperation with anyone with clean aims.
…..
I want say some words to observers who work with other Mirror devices, but not genuine Kozyrev’s Mirrors: Don’t attempt to exploit our experiment for money and business! This is dangerous for future of our civilization!
…..
We have now photo confirmation of the effectiveness of our technology: the Mirror’s quantum superposition of human consciousness. We ‘ll be glad to look at photos and other results of communications from our colleagues.
There are different research projects within the institute, so that the “Kozyrev’s mirrors” project may well be a smoke screenI It is not clear where the Institute is getting money from. Some people working on alternative mirrors speculate that, perhaps, from China (Chineese seems to be, in particular, interested in “magical properties of water”). Years ago money was coming from the government and other secret sources. Nowadays it seems to be a total mess. But I do not have a reliable information.
The page with “News” from the Institute has a beautiful picture of NGC 6357 galaxy that is called “War and Peace”.

The Institute is said to be working on “Starry world without war on Earth”.
Perhaps I should add that the official address of the institute points to just one office in a big building in Novosibirsk that is renting offices:

аренда помещения в Новосибирске, в …Новосибирск, Академика Лаврентьева проспект, д. 6/1, 3000 м2.
As far as I know there is no strong evidence that the (para)psychological/medical phenomena that are observed with the help of aluminium and other mirrors have anything to do with mirrors at all. There are claims that similar effects can be obtained by just imagining being within a mirror – much like placebo effects. The effects seem to depend also on “the operator”. There seems to be a war between the group in Novosibirsk and competitors who also claim to be able to see the future in their version of Kozyrev’s mirrors via “energo-informatic interactions”:

So much about Kozyrev’s mirrors today. Now back to mathematics and physics of the swinging pendulum. According to cosmoplanetary philosophy it may be not the right thing to do, because we should be concentrating our efforts on saving our endangered eco and info space so much polluted by us, human beings, who instead of concentrating on how to “be” are concentrating on how to “have”. But I do not want to have the pendulum, I simply want to know how it works. And after finding it out – I may want to ask further questions like “what is inertia?”, “what is space?” and “what is time?”. But first things first.
It would be a shame to leave our pendulum and move back to gyroscopes without showing first the phase diagram. It is featured on Wikipedi’a page on Pendulum:

Here is another illustration from the book “The chaotic pendulum” by Moshe Gitterman

It would be nice to know how these people got these pictures and what they mean. And we are quite ready for it, it is in fact very very easy. Easier than solving differential equations. In fact these are, in a sense, pictures of the differential equations.
In Rescaled Jacobi amplitude – general solution for the mathematical pendulum we have derived differential equation (Eq. (7)) for ![]()
![]()
which is the same as
![]()
We set ![]() and solve for
and solve for ![]()
(1) ![]()
We have the angular velocity ![]() as a function of
as a function of ![]() and we can plot these functions for different values of
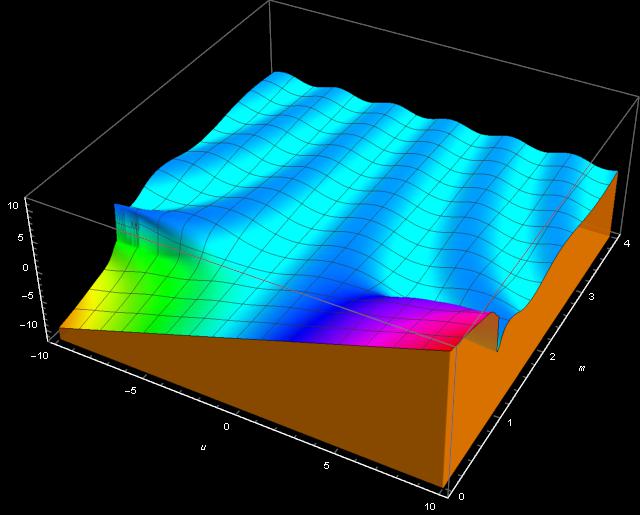
and we can plot these functions for different values of ![]() Here is what I got using Mathematica:
Here is what I got using Mathematica:

Here ![]() and
and ![]() are changing from 1 to 10. Nice picture, I think.
are changing from 1 to 10. Nice picture, I think.
One thought occurs to me: our mathematical pendulum has an arm. It is supposed to be of constant length. Suppose we want to verify our predictions for the period in real experiments. If we make the arm out of steel, it will be hard to make it weightless. But if we make it out of string, then, I think, there will be some minimal angular velocity needed for the string not to collapse under gravity?
 International Journal of Unconventional Science is being translated form Russian to English. Here is what is already available:
International Journal of Unconventional Science is being translated form Russian to English. Here is what is already available:




