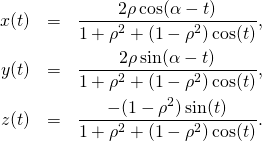“Everything is repeated, in a circle. History is a master because it teaches us that it doesn’t exist. It’s the permutations that matter.” So wrote Umberto Eco in his Focault’s Pendulum. Somehow we, humans, are helping these repetitions to happen. I can see it quite clearly looking at my own adventures. In the previous post we have started our adventure with nuts flipping in space. But very soon I moved to quaternions. Frankly speaking quaternions are not absolutely necessary. We could avoid them and stay with real 3×3 real rotation matrices, known to every engineer. So, why did I call quaternions into teh game? Sure, they are somewhat exotic and cool. That is a good reason. But the truth is that with quaternions I am relating my today’s adventure with Dzhanibekov’s effect to my old adventure with Quantum Fractals. In my monograph on Quantum Fractals
 you can find the following images from quantum theory of pure spin 1/2. These images represent what mathematicians often call ‘Villarceau circles’ and ‘Hopf fibration’.
you can find the following images from quantum theory of pure spin 1/2. These images represent what mathematicians often call ‘Villarceau circles’ and ‘Hopf fibration’.



That was in my quantum past. I really liked the Villarceau circles. They seem to have some magic in them:

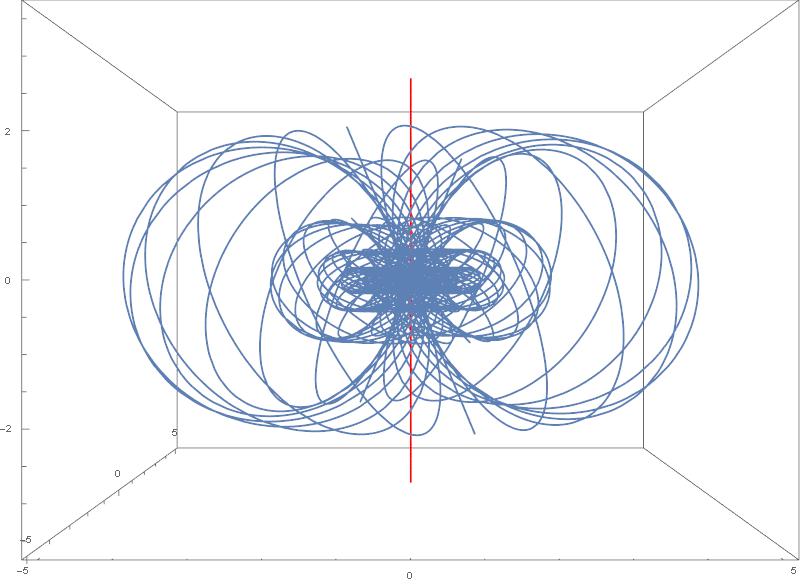
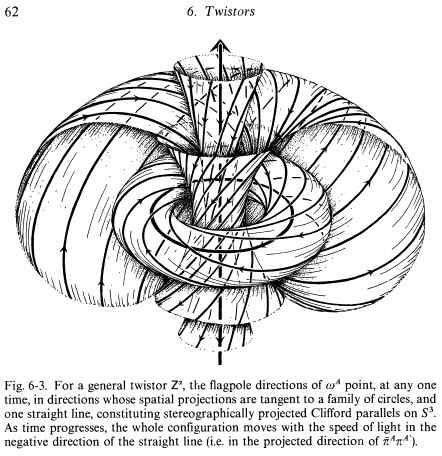
I also like Penrose, Hopf fibration and Clifford parallels
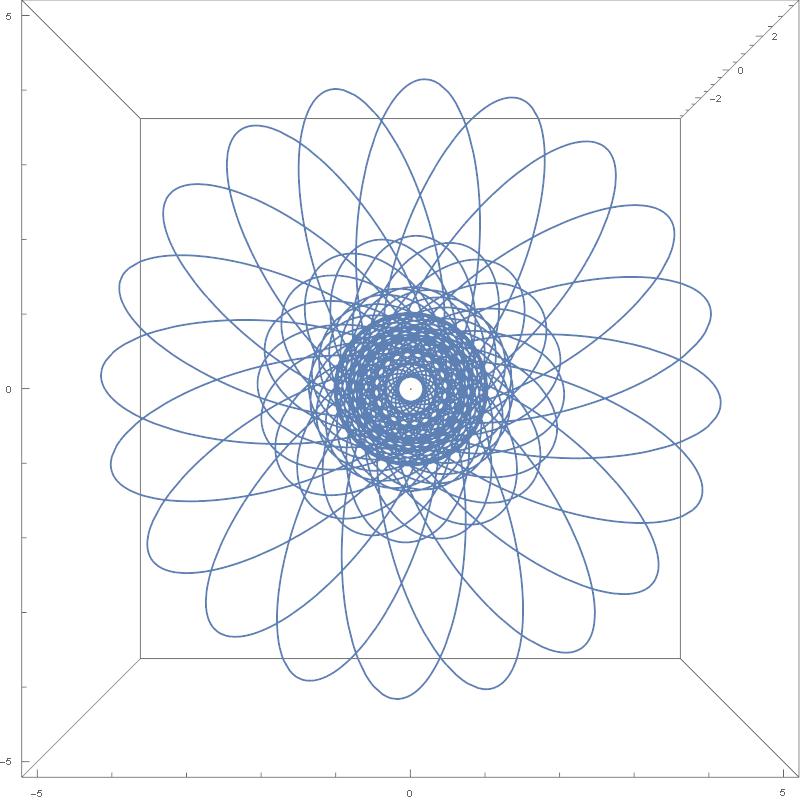
And today, at the end of this post you will see the same structures reappearing – when quaternions are used for rotating the winged nut in space.
Therefore, let us continue from the last post.
In order to visualize the trajectories we do stereographic projection from ![]() with removed one point,
with removed one point, ![]() onto
onto ![]() . Denoting
. Denoting ![]() the coordinates in
the coordinates in ![]() we take
we take
(1) 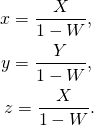
The inverse transformation is given by
(2) 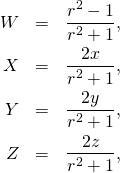
where ![]()
We now take a point ![]() in
in ![]() , transform it into a point
, transform it into a point ![]() on
on ![]() , apply the right shift to obtain
, apply the right shift to obtain ![]() and project to get
and project to get ![]() The result is
The result is
(3) 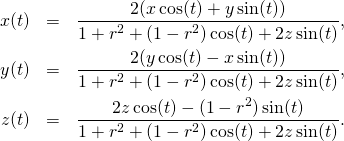
First consider the special trajectory through the origin ![]() therefore
therefore ![]() It is given by
It is given by ![]()
Using trigonometric identities we get ![]() The trajectory is therefore the
The trajectory is therefore the ![]() -axis. It is the stereographic projection of the curve
-axis. It is the stereographic projection of the curve ![]() connecting
connecting ![]() with
with ![]()
The second special case is when ![]() and
and ![]() We get the unit circle in the plane
We get the unit circle in the plane ![]()
(4) 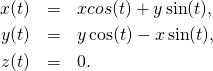
Apart of these two special cases every trajectory intersects the plane ![]() twice. Therefore it is enough to restrict to the trajectories originating at points with
twice. Therefore it is enough to restrict to the trajectories originating at points with ![]() We introduce polar coordinates on the plane
We introduce polar coordinates on the plane ![]() With
With ![]() we set
we set ![]() With
With ![]() the equations for trajectories become:
the equations for trajectories become:
(5)