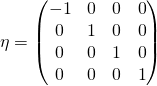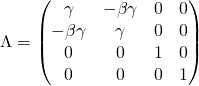From the two-dimensional disk we are moving to three-dimensional space-time. We will meet Einstein-Poincare-Minkowski special relativity, though in a baby version, with x and y, but without z in space. It is not too bad, because the famous Lorentz transformations, with length contraction and time dilation happen already in two-dimensional space-time, with x and t alone. We will discover Lorentz transformations today. First in disguise, but then we will unmask them.
First we recall, from The disk and the hyperbolic model, the relation between the coordinates ![]() on the Poincare disk
on the Poincare disk ![]() , and
, and ![]() on the unit hyperboloid
on the unit hyperboloid ![]()

(1) 
(2) 
We have the group SU(1,1) acting on the disk with fractional linear transformations. With ![]() and
and ![]() in SU(1,1)
in SU(1,1)
(3) ![]()
the fractional linear action is
(4) ![]()
By the way, we know from previous notes that ![]() is in SU(1,1) if and only if
is in SU(1,1) if and only if
(5) ![]()
Having the new point on the disk, with coordinates ![]() we can use Eq. (1) to calculate the new space-time point coordinates
we can use Eq. (1) to calculate the new space-time point coordinates ![]() This is what we will do now. We will see that even if
This is what we will do now. We will see that even if ![]() depends on
depends on ![]() in a nonlinear way, the space-time coordinates transform linearly. We will calculate the transformation matrix
in a nonlinear way, the space-time coordinates transform linearly. We will calculate the transformation matrix ![]() and express it in terms of
and express it in terms of ![]() and
and ![]() We will also check that this is a matrix in the group SO(1,2).
We will also check that this is a matrix in the group SO(1,2).
The program above involves algebraic calculations. Doing them by hand is not a good idea. Let me recall a quote from Gottfried Leibniz, who, according to Wikipedia
He became one of the most prolific inventors in the field of mechanical calculators. While working on adding automatic multiplication and division to Pascal’s calculator, he was the first to describe a pinwheel calculator in 1685[13] and invented the Leibniz wheel, used in the arithmometer, the first mass-produced mechanical calculator. He also refined the binary number system, which is the foundation of virtually all digital computers.

“It is unworthy of excellent men to lose hours like slaves in the labor of calculation which could be relegated to anyone else if machines were used.”
— Gottfried Leibniz
I used Mathematica as my machine. The same calculations can be certainly done with Maple, or with free software like Reduce or Maxima. For those interested, the code that I used, and the results can be reviewed as a separate HTML document: From SU(1,1) to Lorentz.
Here I will provide only the results. It is important to notice that while the matrix ![]() has complex entries, the matrix
has complex entries, the matrix ![]() is real. The entries of
is real. The entries of ![]() depend on real and imaginary parts of
depend on real and imaginary parts of ![]() and
and ![]()
(6) ![]()
Here is the calculated result for ![]() :
:
(7) 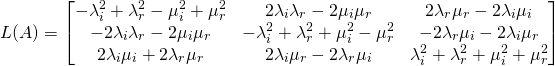
In From SU(1,1) to Lorentz it is first verified that the matrix ![]() is of determinant 1. Then it is verified that it preserves the Minkowski space-time metric. With
is of determinant 1. Then it is verified that it preserves the Minkowski space-time metric. With ![]() defined as
defined as
(8) 
we have
(9) ![]()
Since ![]() the transformation
the transformation ![]() preserves the time direction. Thus
preserves the time direction. Thus ![]() is an element of the proper Lorentz group
is an element of the proper Lorentz group ![]() .
.
Remark: Of course we could have chosen ![]() with
with ![]() on the diagonal. We would have the group SO(2,1), and we would write the hyperboloid as
on the diagonal. We would have the group SO(2,1), and we would write the hyperboloid as ![]() It is a question of convention.
It is a question of convention.
In SU(1,1) straight lines on the disk we considered three one-parameter subgroups of SU(1,1):
(10) 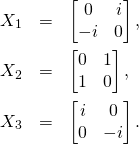
(11) 
We can now use Eq. (7) in order to see which space-time transformations they implement. Again I calculated it obeying Leibniz and using a machine (see From SU(1,1) to Lorentz).

Here are the results of the machine work:
(12) 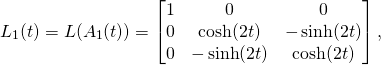
(13) 
(14) 
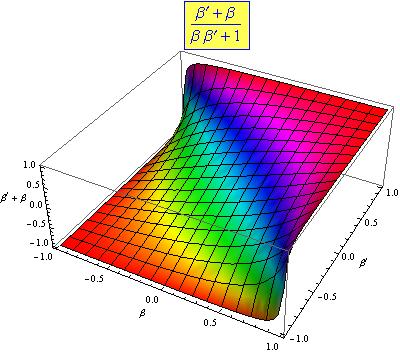
The third family is a simple Euclidean rotation in the ![]() plane. That is why I denoted the parameter with the letter
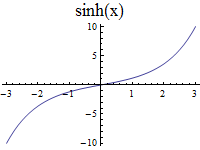
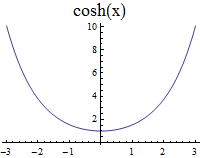
plane. That is why I denoted the parameter with the letter ![]() In order to “decode” the first two one-parameter subgroups it is convenient to introduce new variable
In order to “decode” the first two one-parameter subgroups it is convenient to introduce new variable ![]() and set
and set ![]() The group property
The group property ![]() is then lost, but the matrices become evidently those of special Lorentz transformations,
is then lost, but the matrices become evidently those of special Lorentz transformations, ![]() transforming
transforming ![]() and
and ![]() , leaving
, leaving ![]() unchanged, and
unchanged, and ![]() transforming
transforming ![]() and leaving
and leaving ![]() unchanged (though with a different sign of
unchanged (though with a different sign of ![]() ). Taking into account the identities
). Taking into account the identities
(15) 
we get
(16) 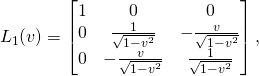
(17) 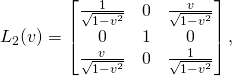
In the following posts we will use the relativistic Minkowski space distance on the hyperboloid for finding the distance formula on the Poincare disk.