This is a continuation from Dedekind tessellation or circles all the way down. I am studying the very interesting paper by J. Kocik, aka Jurek, “A note on the Dedekind tessellation”. It is a pity that the paper is unpublished. I am not sure how much of its content I am allowed to reveal. I will take a risk and reveal just one goodie from this paper.
Here is the goodie:
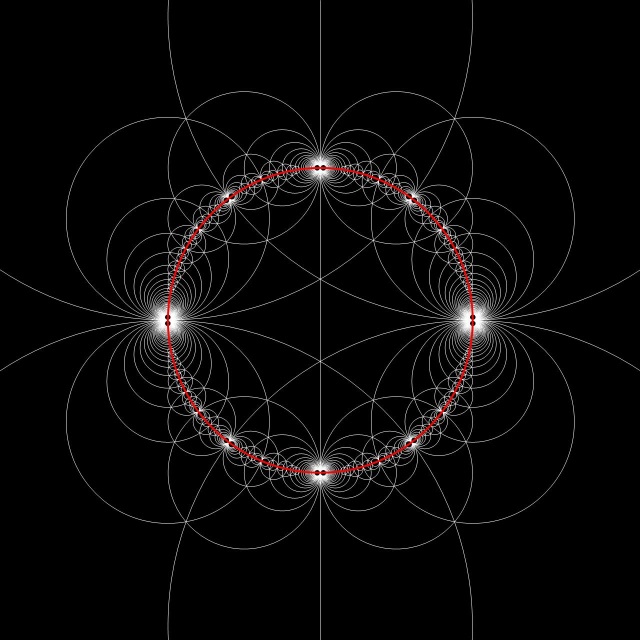
Click on the image to open in full resolution.
And I will explain now how I produced this picture.
As I have explained it in Dedekind tessellation or circles all the way down, we have a nice tessellation of the upper half-plane. The upper half-plane is tessellated by circles which, in hyperbolic geometry are “straight lines”. Using Cayley transform we can move these circles to the unit disk. Kocik, in his paper, gives the algorithm for constructing the centers and the radii of these circles. I used Mathematica to implement this algorithm as follows:

I did not follow exactly Kocik’s algorithm. Moreover I have rotated the data from his paper by 90 degrees, so that it agrees with the Cayley transform I was using before. I stored the list of positions and radii of the circles that I was using in a file: c200.m.
The red circle is the unit circle. Strictly speaking the Dedekind tessellation should be restricted to the inside of the unit circle. But It is amazing to plot the circles also in the outside region. After all the unit circle is just a boundary between two universes. Why should we restrict ourselves to only one side? The universe we are living in is, perhaps, also a boundary between different multidimensional universes of hyperdimensional physics.




