Riemannian metric is usually expressed through its metric tensor. For instance in Conformally Euclidean geometry of the upper half-plane we were discussing the SL(2,R) invariant Riemannian metric on the upper half-plane and came out with the formula:
(1) ![]()
Riemannian metric in ![]() dimensions is given by
dimensions is given by ![]() symmetric matrix
symmetric matrix ![]() The components of this matrix are, in general, functions of coordinates of the points of the space under consideration. Knowing the metric, we can calculate scalar product of any two tangent vectors at the same point. Knowing the scalar product of any two vectors we can calculate the metric tensor. It goes as follows. Suppose we have coordinates
The components of this matrix are, in general, functions of coordinates of the points of the space under consideration. Knowing the metric, we can calculate scalar product of any two tangent vectors at the same point. Knowing the scalar product of any two vectors we can calculate the metric tensor. It goes as follows. Suppose we have coordinates ![]() . Sometimes the coordinates have their names, like
. Sometimes the coordinates have their names, like ![]() but then it is often convenient to number them, for instance
but then it is often convenient to number them, for instance ![]() , and to refer to them through their indices. When we have coordinates, we have vectors tangent to the coordinate lines. They are usually denoted as
, and to refer to them through their indices. When we have coordinates, we have vectors tangent to the coordinate lines. They are usually denoted as ![]() or even simply
or even simply ![]() . This is a standard notation used in differential geometry texts. So, for instance,
. This is a standard notation used in differential geometry texts. So, for instance, ![]() is vector tangent to the coordinate line
is vector tangent to the coordinate line ![]() , that is the line when
, that is the line when ![]() is varying while
is varying while ![]() are kept constant. More precisely:
are kept constant. More precisely: ![]() is a vector field, since we can draw the coordinate of
is a vector field, since we can draw the coordinate of ![]() through every point. Therefore when I write
through every point. Therefore when I write ![]() I mean the vector field or I mean one particular vector at one particular point that should be evident from the context. When it needs to be specified, we can write
I mean the vector field or I mean one particular vector at one particular point that should be evident from the context. When it needs to be specified, we can write ![]() – which means that we are specifying particular point
– which means that we are specifying particular point ![]()
If we have scalar product ![]() defined at every point
defined at every point ![]() of our space, then the metric tensor at a point
of our space, then the metric tensor at a point ![]() is given by the matrix
is given by the matrix
(2) ![]()
Vectors ![]() tangent to the coordinate lines form a basis in the tangent space at every point. When we say that a given
tangent to the coordinate lines form a basis in the tangent space at every point. When we say that a given ![]() has components
has components ![]() , that means that
, that means that ![]() – where we use Einstein convention implying summation over the dummy index. Thus we may write:
– where we use Einstein convention implying summation over the dummy index. Thus we may write:
(3) ![]()
We will now calculate explicitly the coordinate expression for the metric on SL(2,R) described in the last post Riemannian metric on SL(2,R).
The coordinates ![]() on the group manifold were introduced in Parametrization of SL(2,R) through
on the group manifold were introduced in Parametrization of SL(2,R) through
(4) 
Let us now find the vector fields tangent to the coordinate lines:
(5) 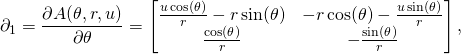
(6) 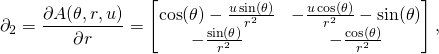
(7) ![]()
These are tangent vectors at ![]() . According to the prescription described in Riemannian metric on SL(2,R) we need to shift them to the identity, that is we need to calculate
. According to the prescription described in Riemannian metric on SL(2,R) we need to shift them to the identity, that is we need to calculate ![]() , and then take trace of their products:
, and then take trace of their products:
(8) ![]()
I did these calculations using computer. Here are the results:
(9) 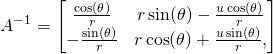
(10) ![]()
(11) 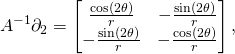
(12) 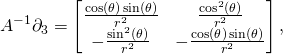
(13) 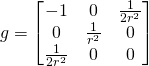
The metric is not diagonal. That means the coordinate lines are not all perpendicular to each other. Moreover, the third line is “light-like”. We have ![]() In Minkowski space-time it would mean that it is a trajectory of an object moving with the speed of light. At the group identity we have
In Minkowski space-time it would mean that it is a trajectory of an object moving with the speed of light. At the group identity we have ![]() At this point we have
At this point we have
(14) ![]()
In SL(2,R) generators and vector fields on the half-plane we have denoted this generator as ![]() .
.
Once we have the metric, we can now calculate its geodesics and curvature. So, we have a plan for the following notes.



It was bad. Thanks.
I don’t understand eguation (14).
Where it comes from?
Now it comes from (7) for r=1, theta=0.
Before there was a mistake. Fixed. Thanks.
“When we have coordinates, we have vectors tangent to the coordinate lines. They are usually denoted as or even simply
or even simply  .”
.”
Do those vectors are only tangent or have also specific length?
Specific length. Is defined as the partial derivative with respect to the given coordinate. When you scale the coordinate, the derivative automatically scales.