Whenever we have a matrix Lie group, we also have its infinitesimal generators. From generators we get group elements by exponentiation. Generators form a linear space. In fact they form algebra with respect to commutators. In our case, for the groups SU(1,1) and SL(2,R), the Lie algebras are three-dimensional. We can choose there three linearly independent generators that form a linear basis for the whole algebra. From exponentials of generators we can form one-parameter subgroups. When the group acts on some space, like SU(1,1) on the disk ![]() , or SL(2,R) on the half-space
, or SL(2,R) on the half-space ![]() , one parameter subgroups define orbits – streamlines of the corresponding vector fields. Here are the details.
, one parameter subgroups define orbits – streamlines of the corresponding vector fields. Here are the details.
Suppose ![]() is a path in the group SL(2,R). Suppose at
is a path in the group SL(2,R). Suppose at ![]() we have
we have ![]() For all
For all ![]() we have
we have ![]() Let
Let ![]() be the derivative of
be the derivative of ![]() with respect to
with respect to ![]() at
at ![]() Then
Then ![]() This follows from the general identity valid for matrix functions
This follows from the general identity valid for matrix functions ![]() with invertible
with invertible ![]() (see e.g. here)
(see e.g. here)
(1) ![]()
When ![]() and
and ![]() then
then ![]() We have already met this property when discussing the group SU(1,1) in Getting hyperbolic
We have already met this property when discussing the group SU(1,1) in Getting hyperbolic
The set of all tangent vectors ![]() at identity is called the Lie algebra of the group. In our case the Lie algebra of SL(2,R) consists of all real
at identity is called the Lie algebra of the group. In our case the Lie algebra of SL(2,R) consists of all real ![]() matrices with trace zero. It is denoted sl(2,R). The elements of sl(2,R) are called “generators” of the group. If
matrices with trace zero. It is denoted sl(2,R). The elements of sl(2,R) are called “generators” of the group. If ![]() is a generator, that is, in our case, if
is a generator, that is, in our case, if ![]() then
then ![]() is a one-parameter subgroup of the group. That
is a one-parameter subgroup of the group. That ![]() follows from another useful identity that can be found in Wikipedia under the term The determinant of the matrix exponential:
follows from another useful identity that can be found in Wikipedia under the term The determinant of the matrix exponential:
(2) ![]()
The Lie algebra of group is an “algebra” with respect to the commutator operation. In our case if ![]() and
and ![]() are matrices in sl(2,R), then
are matrices in sl(2,R), then ![]() is also in sl(2,R) because for any two matrices
is also in sl(2,R) because for any two matrices ![]() we have that
we have that ![]() Thus trace of a commutator is always zero.
Thus trace of a commutator is always zero.
In SU(1,1) straight lines on the disk we met these SU(1,1) generators (I am changing the sign of ![]() here)
here)
(3) 
In Getting real the Cayley transform was defined using the matrix ![]()
(4) ![]()
(5) ![]()
The transformation ![]() maps the group SU(1,1) onto the group SL(2,R). The same transformation maps the Lie algebra su(1,1) onto the Lie algebra sl(2,R). In particular we obtain the following three generators in sl(2,R):
maps the group SU(1,1) onto the group SL(2,R). The same transformation maps the Lie algebra su(1,1) onto the Lie algebra sl(2,R). In particular we obtain the following three generators in sl(2,R):
(6) 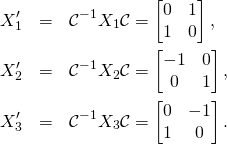
We can take exponentials of these generators and construct one-parameter subgroups
(7) 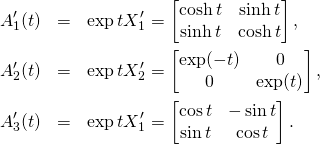
From these we can define their orbits in the half-plane:
(8) 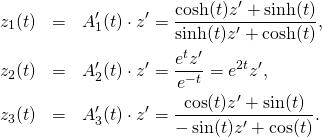
Differentiating with respect to ![]() at
at ![]() we obtain vector fields. I will use the tilde symbol to denote these vector fields. I will be skipping primes from this place on.
we obtain vector fields. I will use the tilde symbol to denote these vector fields. I will be skipping primes from this place on.
(9) 
Here are streamlines of these three vector fields.
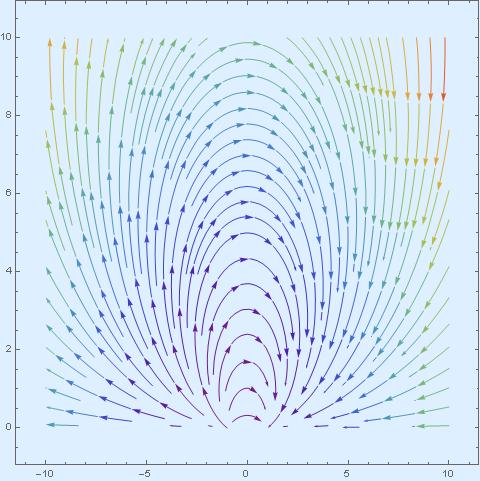
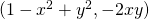 on the half-plane
on the half-plane 
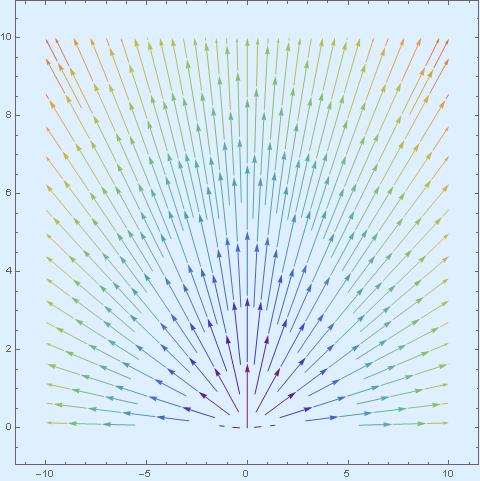
 on the half-plane
on the half-plane 
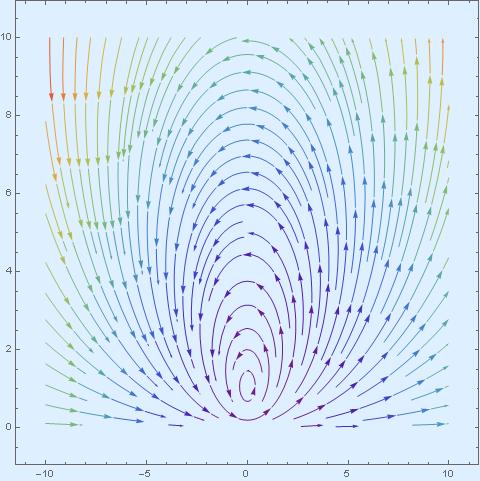
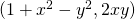 on the half-plane
on the half-plane 
While the second vector field produces very simple streamlines, the first and the third are kind of strange.
Looking at Eqs. (6) we see, that it may be wise to introduce the linear combinations as follows:
(10) 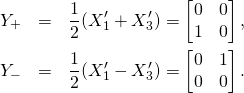
Now ![]() and
and ![]() are nilpotents (that is their squares are zero), therefore taking exponentials is easy:
are nilpotents (that is their squares are zero), therefore taking exponentials is easy:
(11) 
We are not going to worry about ![]() but using
but using ![]() proves to be an excellent idea! The corresponding orbits on the half-plane are extremely simple
proves to be an excellent idea! The corresponding orbits on the half-plane are extremely simple
(12) ![]()
The corresponding vector field is
(13) ![]()
Here are the corresponding streamlines:
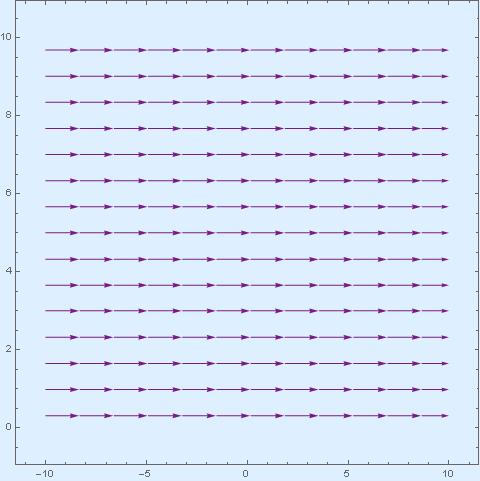
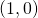 on the half-plane
on the half-plane 
We will exploit ![]() and
and ![]() in the future. Their interpretation is very simple. The first one describes uniform dilation. Expanding (or contracting) in horizontal and in vertical direction at the same rate. The second one is a uniform horizontal translation. The hyperbolic geometry of the plane needs to be invariant with respect to these two kinds of transformations.
in the future. Their interpretation is very simple. The first one describes uniform dilation. Expanding (or contracting) in horizontal and in vertical direction at the same rate. The second one is a uniform horizontal translation. The hyperbolic geometry of the plane needs to be invariant with respect to these two kinds of transformations. If that is so, then it is invariant with respect to the whole SL(2,R) group, because the third generator can be obtained from these two and their commutator!






Trzeci obrazek:
(+-x^2-y^2, 2xy)
chyba miało być:
(1+x^2-y^2, 2xy)
Tak. Dziękuję.
“The set of all tangent vectors at identity …”
at identity …”
?
We assume , so at
, so at 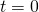 the curve passes the identity. Therefore the tangent vector to the curve is tangent at this point.
the curve passes the identity. Therefore the tangent vector to the curve is tangent at this point.
As for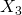 – my
– my 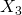 here has a different sign – I have added this note in the text.
here has a different sign – I have added this note in the text.
Thanks.
Thanks!
Thanks.
Above I mentioned forth misspelling:
second vector fields ->
second vector field
(Don’t you agree with that?)
I agree. Thanks.