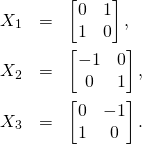In the last post we were discussing Killing vector fields of the group SL(2,R). It was done without specifying any reason for doing it – except that it somehow came in our way naturally. But now there is an opportunity to relate our theme to something that is fashionable in theoretical physics: holographic principle and AdS/CFT correspondence
We were playing with AdS without knowing it. Here AdS stands for “anti-de-Sitter” space. Let us therefore look into the content of one pedagogical paper dealing with the subject: “Anti de Sitter space, squashed and stretched” by Ingemar Beengtsson and Patrik Sandrin . We will not be squashing and stretching – not yet. Our task is “to connect” to what other people are doing. Let us start reading Section 2 of the paper “Geodetic congruence in anti-de Sitter space“. There we read:
For the 2+1 dimensional case the definition can be reformulated in an interesting way. Anti-de Sitter space can be regarded as the group manifold of
, that is as the set of matrices
(1)
It is clear that every SL(2,R) matrix ![]() can be uniquely written in the above form.
can be uniquely written in the above form.
But Section 2 starts with something else:
\noindent Anti-de Sitter space is defined as a quadric surface embedded in a flat space of signature
. Thus 2+1 dimensional anti-de Sitter space is defined as the hypersurface
(2)
\noindent embedded in a 4 dimensional flat space with the metric
(3)
\noindent The Killing vectors are denoted
,
, and so on. The topology is now
, and one may wish to go to the covering
space in order to remove the closed timelike curves. Our arguments
will mostly not depend on whether this final step is taken.For the 2+1 dimensional case the definition can be reformulated in an interesting way. Anti-de Sitter space can be regarded as the group manifold of
, that is as the set of matrices
(4)
\noindent The group manifold is equipped with its natural metric, which is invariant under transformations
,
. The Killing vectors can now be organized into two orthonormal and mutually commuting sets,
(5)
\noindent They obey
(6)
The story here is this: ![]() real matrices form a four-dimensional real vector space. We can use
real matrices form a four-dimensional real vector space. We can use ![]() or
or ![]() as coordinates
as coordinates ![]() there. The condition of being of determinant one defines a three-dimensional hypersurface in
there. The condition of being of determinant one defines a three-dimensional hypersurface in ![]() We can endow
We can endow ![]() with scalar product determined by the matrix
with scalar product determined by the matrix ![]() defined by:
defined by:
(7) 
The scalar product is then defined as
(8) ![]()
This scalar product is invariant with respect to the group SO(2,2) of ![]() real matrices
real matrices ![]() satisfying:
satisfying:
(9) ![]()
That is, if ![]() then
then ![]() for all
for all ![]() in
in ![]()
What I will be writing now is “elementary”in the sense that “everybody in the business” knows it, and if asked will often not be able to tell where and when she/he learned it. But this is a blog, and the subject is so pretty that it would be a pity if people “not in the business” would miss it.
The equation (2) can then be written as ![]() It determines a “generalized hyperboloid” in
It determines a “generalized hyperboloid” in ![]() that is invariant with respect to the action of O(2,2). Thus the situation is analogous to the one we have seen in The disk and the hyperbolic model. There we had the Poincaré disk realized as a two-dimensional hyperboloid in a three-dimensional space with signature (2,1), here we have SL(2,R) realized as a generalized hyperboloid in four-dimensional space with signature (2,2). Before it was the group O(2,1) that was acting on the hyperboloid, now is the group O(2,2). Let us look at the vector fields of the generators of this group. By differentiating Eq. (9) at group identity we find that each generator
that is invariant with respect to the action of O(2,2). Thus the situation is analogous to the one we have seen in The disk and the hyperbolic model. There we had the Poincaré disk realized as a two-dimensional hyperboloid in a three-dimensional space with signature (2,1), here we have SL(2,R) realized as a generalized hyperboloid in four-dimensional space with signature (2,2). Before it was the group O(2,1) that was acting on the hyperboloid, now is the group O(2,2). Let us look at the vector fields of the generators of this group. By differentiating Eq. (9) at group identity we find that each generator ![]() must satisfy the equation:
must satisfy the equation:
(10) ![]()
This equation can be also written as
(11) ![]()
Thus ![]() must be antisymmetric. In
must be antisymmetric. In ![]() dimensions the space of antisymmetric matrices is
dimensions the space of antisymmetric matrices is ![]() -dimensional. For us
-dimensional. For us ![]() therefore the Lie algebra so(2,2) is 6-dimensional, like the Lie algebra so(4) – they are simply related by matrix multiplication
therefore the Lie algebra so(2,2) is 6-dimensional, like the Lie algebra so(4) – they are simply related by matrix multiplication ![]() We need a basis in so(2,2), so let us start with a basis in so(4). Let
We need a basis in so(2,2), so let us start with a basis in so(4). Let ![]() denote the elementary antisymmetric matrix that has
denote the elementary antisymmetric matrix that has ![]() in row
in row ![]() , column
, column ![]() and
and ![]() in row
in row ![]() column
column ![]() for
for ![]() , and zeros everywhere else. In a formula
, and zeros everywhere else. In a formula
![]()
where ![]() is the Kronecker delta symbol:
is the Kronecker delta symbol: ![]() for
for ![]() and
and ![]() for
for ![]()
As we have mentioned above, the matrices ![]() form then the basis in the Lie algebra so(2,2). We can list them as follows
form then the basis in the Lie algebra so(2,2). We can list them as follows
(12) ![]()
(13) ![]()

In the next post we will relate these generators to ![]() from the Anti de Sitter paper by Bengtsson et al and to our Killing vector fields
from the Anti de Sitter paper by Bengtsson et al and to our Killing vector fields
![]() from the last note
from the last note