According to Wikipedia
In differential geometry, a geodesic is a generalization of the notion of a “straight line” to “curved spaces”.
…
The first line in the online Encyclopedia of mathematics is similar
The notion of a geodesic line (also: geodesic) is a geometric concept which is a generalization of the concept of a straight line (or a segment of a straight line) in Euclidean geometry to spaces of a more general type.
…
Wolfram’s MathWorld is somewhat more original:
A geodesic is a locally length-minimizing curve. Equivalently, it is a path that a particle which is not accelerating would follow. In the plane, the geodesics are straight lines. On the sphere, the geodesics are great circles (like the equator). The geodesics in a space depend on the Riemannian metric, which affects the notions of distance and acceleration.
…
It is time for us to study geodesics on the upper half-plane, and do it in a semi-rigorous way. That would require a rigorous definition of geodesics, which would take us into differential geometry and variational calculus. That would certainly not be a length-minimizing and straight way of achieving our goal. For us, interested mainly in Lie groups and their actions, there is a shorter way. It is like in classical mechanics, where in many important cases we do not have to solve complicated Newton’s differential equations, it is enough to use the law of conservation of energy, or momentum.
That is what we will do. We will use conservation laws. Usually these come as theorems in courses of differential geometry (Noether’s theorem). For instance Sean Carroll in his online book Lecture Notes on General Relativity, in Chpater 5, More geometry has this piece:

And that is what we will use. And how to use it, in detail, we will see below.
Let us start with this sentence:
If a one-parameter family of isometries is generated by a vector field
, then
is known as a Killing vector field.
We have our candidates for Killing vector fields. We were plotting some of their streamlines in SL(2,R) generators and vector fields on the half-plane .
But are we sure that they generate “isometries”? Till now we have only a roundabout argument: metric on the upper half-plane comes from the metric on the disk, metric on the disk comes from geometry on the hyperboloid, metric on the hyperboloid comes from flat space-time metric of signature ![]() and the SL(2,R) group comes from the SO(2,1) group of linear transformations preserving the flat space-time metric. That could be enough for a while, but can’t we check directly if indeed we have isometries?
and the SL(2,R) group comes from the SO(2,1) group of linear transformations preserving the flat space-time metric. That could be enough for a while, but can’t we check directly if indeed we have isometries?
Yes, we can check, and that is, in fact, quite easy. Generators of the SL(2,R) group form the Lie algebra sl(2,R) of real ![]() matrices of trace zero. After exponentiation they generate one-parameter groups of SL(2,R) matrices. SL(2,R) acts on the upper-half plane
matrices of trace zero. After exponentiation they generate one-parameter groups of SL(2,R) matrices. SL(2,R) acts on the upper-half plane ![]() by linear fractional transformations. If
by linear fractional transformations. If ![]() is in SL(2,R)
is in SL(2,R)
(1) ![]()
(2) ![]()
Is the transformation defined in Eq. (2) an isometry? The formula looks relatively simple when written in terms of complex variables. But if we write ![]() then the coordinates
then the coordinates ![]() of the transformed point become not that simple functions of the coordinates
of the transformed point become not that simple functions of the coordinates ![]() of the original point:
of the original point:
(3) ![]()
(4) ![]()
Is it an isometry? And what is isometry?
In Conformally Euclidean geometry of the upper half-plane we have derived the formula for calculating the length of a given curve:
(5) ![]()
Now, suppose, we transform our curve using the matrix ![]() . The length of the transformed curve is then given by the formula
. The length of the transformed curve is then given by the formula
(6) 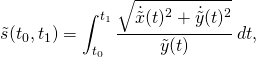
where the relation between ![]() and
and ![]() is given by Eqs. (3,4).
is given by Eqs. (3,4).
The transformation is an isometry if ![]() for any segment of any curve. Is true in our case? In order to verify it some little calculations are needed. If we listen to Leibniz:
for any segment of any curve. Is true in our case? In order to verify it some little calculations are needed. If we listen to Leibniz:

— Gottfried Leibniz
we use our computer. I used Mathematica. Here is the result:

To summarize: after somewhat lengthy calculation we end up with
(7) ![]()
even without using the ![]() condition. Therefore SL(2,R) transformations are indeed isometries (for our metric). Therefore our vector fields are “Killing vector fields”. Therefore we can use their properties in our derivation of geodesic equations. Which we will continue in the following post.
condition. Therefore SL(2,R) transformations are indeed isometries (for our metric). Therefore our vector fields are “Killing vector fields”. Therefore we can use their properties in our derivation of geodesic equations. Which we will continue in the following post.






Thanks!