In the last post, Geodesics of left invariant metrics on matrix Lie groups – Part 1,we have derived Arnold’s equation – that is a half of the problem of finding geodesics on a Lie group endowed with left-invariant metric.
Suppose ![]() is a Lie group, and
is a Lie group, and ![]() is a scalar product (i.e. a nondegenerate bilinear form) on its Lie algebra
is a scalar product (i.e. a nondegenerate bilinear form) on its Lie algebra ![]() . Then, using left translations
. Then, using left translations ![]() defines a left invariant (Riemannian or pseudo-Riemannian) metric on the whole group
defines a left invariant (Riemannian or pseudo-Riemannian) metric on the whole group ![]() If
If ![]() is a path in
is a path in ![]() we use left translations to define the image
we use left translations to define the image ![]() of the tangent vector
of the tangent vector ![]() in
in ![]()
(1) ![]()
Usually it is written more carefully, using ![]() instead of
instead of ![]() , but I am using a simplified notation, well adapted to dealing with problems for matrix groups.
, but I am using a simplified notation, well adapted to dealing with problems for matrix groups.
If ![]() is a geodesic for the metric
is a geodesic for the metric ![]() , then
, then ![]() satisfies the Arnold’s equation
satisfies the Arnold’s equation
(2) ![]()
where
![]()
is defined as
(3) ![]()
and ![]() are the structure constants of
are the structure constants of ![]() , that is
, that is
(4) ![]()
where ![]() form a basis for
form a basis for ![]() and
and
(5) ![]()
Equation (2) is a system of nonlinear ordinary differential equations with constant coefficients. In this form it can be found in Arnold’s 1966 paper “Sur la g\’eom\’etrie differentielle des groupes de Lie de dimension infinie et ses applications \`a l’hydrodynamique des fluides parfaits”, Ann. Inst.
Fourier (Grenoble) 16 (1966), 319-361.

In his blog post “The Euler-Arnold equation” Terrence Tao mentions that some people call this equation the “Euler-Arnold” equation, while some other prefer to skip Arnold’s name completely and call it “Euler-Poincare equation”. Go-figure!
Solving equations (2) is just one half of the whole problem of finding a geodesic. Once ![]() are known, we need to solve the linear differential equation with variable coefficients that results from the definition of
are known, we need to solve the linear differential equation with variable coefficients that results from the definition of ![]() (??):
(??):
(6) ![]()
For the case of the rotation group and free rigid body we did it in Taming the T-handle continued.
B. Kolev in his paper “Lie groups and mechanics. An introduction” shows that for the rotation group O(n) the equations of motion for the free rigid body are completely integrable. We will not need this result, but is useful to know that in general case there are always two quadratic constants of motion corresponding to “kinetic energy” and “square of the angular momentum”. We were discussing these constants of motion for the group O(3) in
“Asymmetric Spinning Top – The Hardest Concept To Grasp In Physics” – they are used in so-called Poinsot construction. We will discuss a version of it for the group O(2,1) in the future.
The first observation is that the “kinetic energy” ![]() is, in fact, a constant, independent of
is, in fact, a constant, independent of ![]() To see that this is the case, we differentiate:
To see that this is the case, we differentiate:
(7) ![]()
In the previous post we wrote Eq. (2) as
(8) ![]()
Substituting into Eq. (7) we get
(9) ![]()
The result is zero because ![]() is antisymmetric in
is antisymmetric in ![]() while
while ![]() is symmetric. That is an often used property: if
is symmetric. That is an often used property: if ![]() and
and ![]() then the contraction
then the contraction ![]() Indeed
Indeed ![]() where in the last equality we have exchanged dummy indices names
where in the last equality we have exchanged dummy indices names ![]() . If a number is equal to its negative, it must be zero.
. If a number is equal to its negative, it must be zero.
To get the formula for the second quadratic invariant we need to return to the Ad-invariant scalar product that we have denoted ![]() in Killing vectors, geodesics, and “Noether’s theorem”:
in Killing vectors, geodesics, and “Noether’s theorem”:
(10) ![]()
The fact that ![]() is Ad-invariant implies an important relation between the matrix
is Ad-invariant implies an important relation between the matrix ![]() and the structure constants
and the structure constants ![]()
that we are going to use. Ad-invariance means that:
(11) ![]()
for all ![]() and
and ![]()
Differentiating at ![]() we get
we get
(12) ![]()
Setting ![]() we get
we get
(13) ![]()
Multiplying both sides by ![]() we obtain
we obtain
(14) ![]()
We can now derive the second conservation law. The angular momentum ![]() is defined as
is defined as
(15) ![]()
Notice that ![]() is a covector, a one-form on
is a covector, a one-form on ![]() , it is in the dual
, it is in the dual ![]() of
of ![]() It is the metric that connects the space to its dual. While vectors in
It is the metric that connects the space to its dual. While vectors in ![]() play an active role, they generate transformations, elements in the dual, one-forms from
play an active role, they generate transformations, elements in the dual, one-forms from ![]() , are “passive”, they evaluate vectors to numbers. It is the metric that is the third element here, that allows the active principle to connect to the passive principle. The metric depends on the mass distribution. In application to rigid bodies the inertia tensor is encoded in the metric on the rotation group.
, are “passive”, they evaluate vectors to numbers. It is the metric that is the third element here, that allows the active principle to connect to the passive principle. The metric depends on the mass distribution. In application to rigid bodies the inertia tensor is encoded in the metric on the rotation group.
The second conservation law states that the square of the angular momentum evaluated with the Ad-invariant metric ![]() is constant:
is constant:
(16) ![]()
To verify we differentiate and use Eq. (8) rewritten as
(17) ![]()
(18) ![]()
Now, according to Eq. (14) ![]() is antisymmetric in
is antisymmetric in ![]() , while the product
, while the product ![]() is symmetric, therefore we get zero:
is symmetric, therefore we get zero:
(19) ![]()
In the following posts we will first return to the case of the rotation group in three dimensions and the rigid body, and then try to apply a similar reasoning to the case of the Lorentz group O(2,1) in 2+1 dimensions.

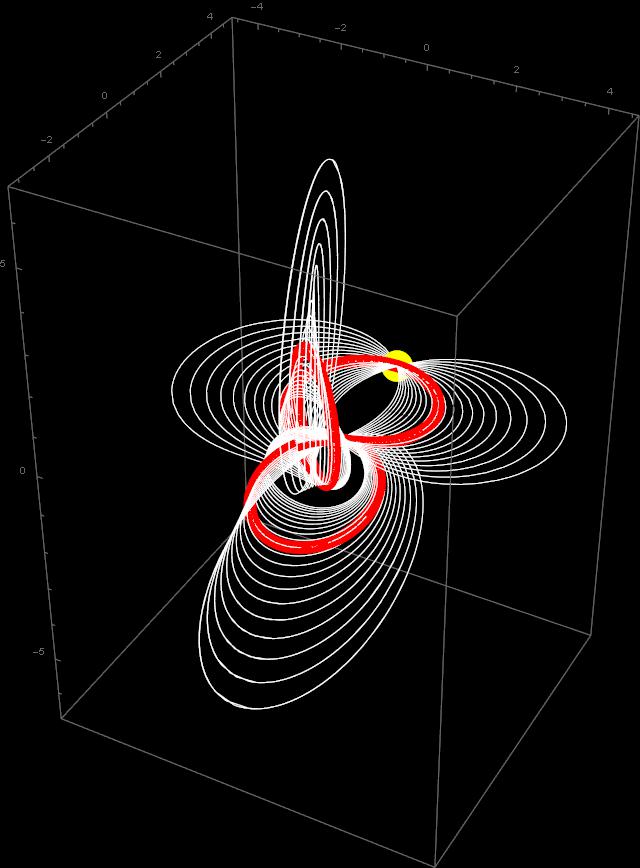







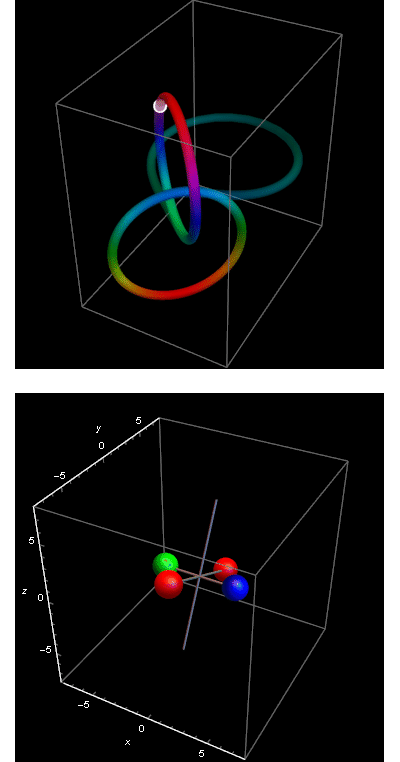
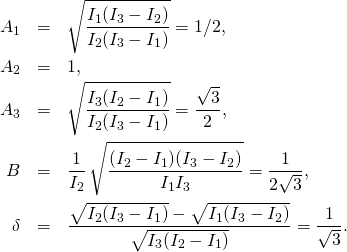


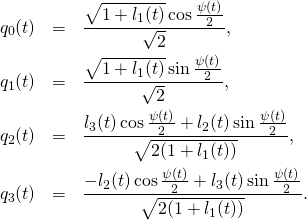
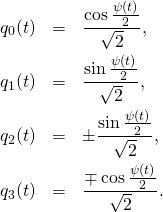
 eternal return”.
eternal return”.