What can we do with Cayley transform? We can produce interesting pictures. Here are two such pictures:
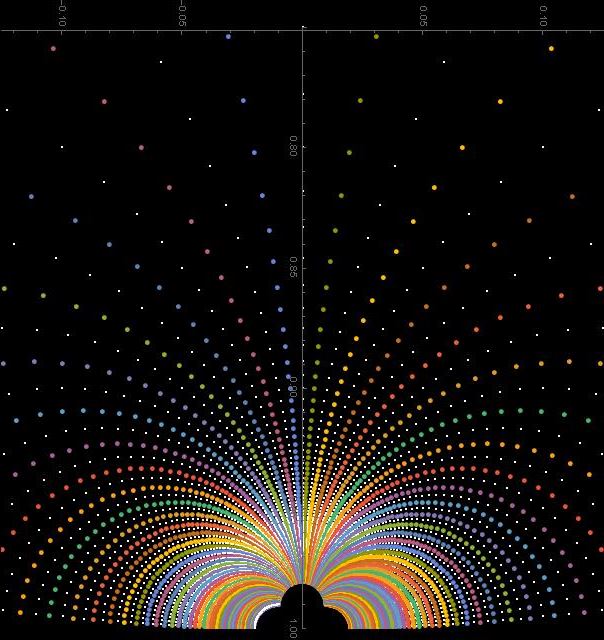
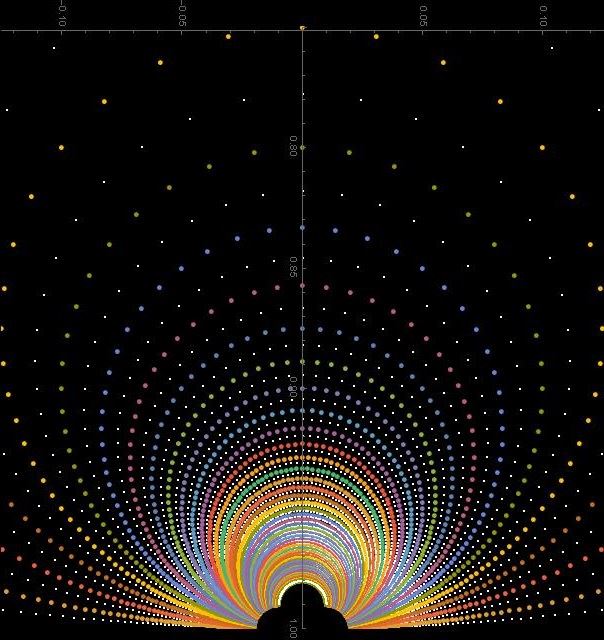
In fact in both pictures we have the same pattern of dots, but they are organized differently by coloring.
How are these images produced? They are produced using Gaussian integers and Cayley transform.
Cayley transform we know from the previous post Cayley transform for Easter. It is the same as in Wikipedia , where it is defined as
(1) ![]()
It maps complex upper half-plane ![]() , the set of all complex numbers with positive imaginary part, onto the interior
, the set of all complex numbers with positive imaginary part, onto the interior ![]() of the unit disk. The real axis is mapped onto the unit circle, minus the point
of the unit disk. The real axis is mapped onto the unit circle, minus the point ![]() The inverse Cayley transform maps
The inverse Cayley transform maps ![]() to infinity.
to infinity.
Gaussian integers are also explained in Wikipedia: \url{}
In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. ….
We want our Gaussian integers to be in ![]() , or on the real line, so we take the integer defining the imaginary part to be nonnegative. To produce images above I took Gaussian integers of the form
, or on the real line, so we take the integer defining the imaginary part to be nonnegative. To produce images above I took Gaussian integers of the form ![]() with m varying from -100 to 100, and
with m varying from -100 to 100, and ![]() varying from 0 to 100. To each such
varying from 0 to 100. To each such ![]() I apply the Cayley transform and plot the point
I apply the Cayley transform and plot the point ![]()
At the end I rotate the images 90 degrees clockwise, so that the neighborhood of ![]() is at the bottom. It looks for me more interesting this way.
is at the bottom. It looks for me more interesting this way.
The colors of the points are constant, either along increasing ![]() or along the increasing
or along the increasing ![]()
Notice that the line with the same color in the first picture look like hyperbolic straight lines – they are circle segments perpendicular to the boundary.
We will need to understand why is it so?






Thank you.