It is Easter Sunday when I writing this note. In Getting real we met the Cayley transform and its inverse.
Namely we have defined the unitary matrix ![]()
(1) ![]()
(2) ![]()
We will use the matrix ![]() in two ways: either for implementing a similarity transformation
in two ways: either for implementing a similarity transformation ![]() resp.
resp. ![]() , or for implementing fractional linear transformation of the type
, or for implementing fractional linear transformation of the type
(3) ![]()
In each case a factor, such as ![]() in front of the matrix is not important. It will cancel out. Two proportional matrices implement the same similarity transformation and the same fractional linear transformation. We have chosen the factor so as to have
in front of the matrix is not important. It will cancel out. Two proportional matrices implement the same similarity transformation and the same fractional linear transformation. We have chosen the factor so as to have ![]() unitary of determinant 1, but that fact will play no role. What is important is the internal structure of
unitary of determinant 1, but that fact will play no role. What is important is the internal structure of ![]()
In Getting real we have found that the similarity transformation
![]()
transforms complex SU(1,1) matrices into real SL(2,R) matrices. Let us now check the fractional linear transformation implemented by ![]() For a general case it is convenient to denote the fractional linear transformation (3) as
For a general case it is convenient to denote the fractional linear transformation (3) as ![]() From Eq. (3) it can be easily verified that, whenever the results are finite, we have
From Eq. (3) it can be easily verified that, whenever the results are finite, we have
(4) ![]()
One could extend the domain and the range of the transformation by replacing the complex plane by its one-point compactification, the Riemann sphere, but we will not need such an extension.
For us the crucial observation is that the transformation ![]() maps the unit disk
maps the unit disk ![]() onto the upper half-plane
onto the upper half-plane ![]() that is onto the set of complex numbers with positive imaginary part. To see this let us examine the properties of
that is onto the set of complex numbers with positive imaginary part. To see this let us examine the properties of ![]() defined by
defined by
(5) ![]()
The imaginary part of ![]() is evidently positive when
is evidently positive when ![]() It becomes zero when
It becomes zero when ![]() Conversely, the transformation
Conversely, the transformation ![]() maps the upper half-plane
maps the upper half-plane ![]() in
in ![]() To see that this is indeed the case let us calculate
To see that this is indeed the case let us calculate ![]()
(6) ![]()
Now ![]() therefore if
therefore if ![]() then
then
(7) ![]()
Moreover, if ![]() that is if
that is if ![]() is on the real axis, then its image
is on the real axis, then its image ![]() is on the unit circle.
is on the unit circle.
We finish this Eater post with an ornament. Consider complex numbers ![]() of the form
of the form ![]() where
where ![]() are real integers with
are real integers with ![]() and
and ![]() Apply the Cayley transform to each such number and plot the number
Apply the Cayley transform to each such number and plot the number ![]() as a point in the disk. Of course we have to restrict the size of
as a point in the disk. Of course we have to restrict the size of ![]() say to
say to ![]() The result is the following Easter Ornament:
The result is the following Easter Ornament:






Czy ta różnica między między wschodem a zachodem jest ok?
(przy okazji – jak z polskimi znakami? Używać, czy lepiej nie?)
Może gdyby ograniczenia na m,n,p,q były inne to tej różnicy by nie było.
Tak, jest to wynik ograniczenia na iloczyn pq. Bez tego ograniczenia jajo byłoby symetryczne, Wschód wygladałby tak samo jak Zachód.
Załapane. Dzięki.
It becomes zero when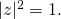
proof needed.
If with
with  real, then
real, then  is the real part and
is the real part and 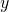 the imaginary part of
the imaginary part of  .
.
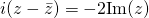 Therefore
Therefore
Therefore, apart of the point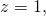 which is singular for this transformation, we are ok.
which is singular for this transformation, we are ok.
Does it answer your question?
Yes. Thanks.