In Parametrization of SL(2,R) we introduced global coordinates ![]() on the group SL(2,R). Any matrix
on the group SL(2,R). Any matrix ![]() in SL(2,R) can be uniquely written as
in SL(2,R) can be uniquely written as
(1) 
If ![]() is the matrix with components
is the matrix with components ![]() then its coordinates can be expressed as functions of the matrix components as follows
then its coordinates can be expressed as functions of the matrix components as follows
(2) 
The function ![]() returns the angle
returns the angle ![]() ,
, ![]() of the complex number
of the complex number ![]()
Once we have coordinates, it is easy to calculate components of tangent vectors to any given path ![]() – they are given by derivatives of the coordinates
– they are given by derivatives of the coordinates ![]() We will calculate now the vector fields resulting from left and right actions of one-parameter subgroups of SL(2,R) that we have already met in SL(2,R) generators and vector fields on the half-plane
We will calculate now the vector fields resulting from left and right actions of one-parameter subgroups of SL(2,R) that we have already met in SL(2,R) generators and vector fields on the half-plane
We have introduced there the one-parameter groups, that we will denote now as ![]() , generated by
, generated by ![]() :
:
(3) 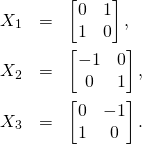
We can take exponentials of the generators and construct one-parameter subgroups
(4) 
In SL(2,R) generators and vector fields on the half-plane we were acting with these transformations on the upper half-plane using fractional linear representation. Now we will be acting on SL(2,R) itself via group multiplication, either left or right.
Let us start with ![]() acting from the left. At
acting from the left. At ![]() we have the trajectory
we have the trajectory ![]() . Its coordinates are
. Its coordinates are ![]() Let us denote by
Let us denote by ![]() the tangent vector field, with components
the tangent vector field, with components ![]() Then
Then
(5) ![]()
We can calculate it easily using algebra software. The result is:
(6) ![]()
The same way we get
(7) ![]()
(8) ![]()
Then we can calculate vector fields of right shifts
(9) ![]()
to obtain:
(10) ![]()
(11) ![]()
(12) ![]()
We know that our metric is bi-invariant. That means the vector fields of the left and right shifts generate one-parameter group of isometries. They are called Killing fields of the metric. In differential geometry one shows that a vector field ![]() is a Killing vector field for metric
is a Killing vector field for metric ![]() if and only if the Lie derivative
if and only if the Lie derivative ![]() of the metric vanishes. Lie derivative of any symmetric tensor
of the metric vanishes. Lie derivative of any symmetric tensor ![]() is defined as
is defined as
(13) ![]()
Using any computer algebra software it is easy to verify that Lie derivatives of our metric with respect to all six vector fields ![]() indeed vanish. Mathematica notebook verifying this property can be downloaded here.
indeed vanish. Mathematica notebook verifying this property can be downloaded here.





Thanks!
Duplicated indexes in eq. (9)
fields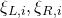 ->
->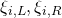
fields
Thanks.