The two-dimensional non-Euclidean hyperbolic geometry that we met is living on the unit disk in the complex plane. Strictly speaking it is living inside the disk, in the disk interior. The unit circle that forms the boundary of the disk is also important, but it is a different story. An interesting and even exciting story, but it does not belong to this particular series. Perhaps it will be enough to mention here that holomorphic functions on the disk attain their extrema on the boundary, thus the circle is a special case of so called Shilov boundary.
We used Cayley transform to move our scene from the disk to the complex half-plane – the set of complex numbers with positive imaginary part. The boundary circle (minus one point) is then mapped onto the real axis. Real axis is the boundary of the half-plane. With Cayley transform, which reads as
(1) ![]()
one point on the boundary, namely ![]() is mapped into infinity. We will not worry about this issue, as we will be mainly interested in the geometry of the interior.
is mapped into infinity. We will not worry about this issue, as we will be mainly interested in the geometry of the interior.
The inverse transform, from the half-plane to the disk is
(2) ![]()
These are the formulas written in terms of complex variables. But studying geometry we usually deal with real variables. If we write ![]() then Eq. (2) can be written as
then Eq. (2) can be written as
(3) 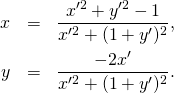
Certainly Eq. (2) looks less complicated than (3) – that is why often using complex notation is convenient. But not always.
In Following Einstein: deriving Riemannian metric on the Poincaré disk we have derived the formula for the line element ![]() of the invariant distance on the disk. In terms of real coordinates
of the invariant distance on the disk. In terms of real coordinates ![]() on the disk the formula that we have derived reads:
on the disk the formula that we have derived reads:
(4) ![]()
How the formula for ![]() will look in terms of the variables
will look in terms of the variables ![]() on the half-plane? Will it be more complicated or simpler?
on the half-plane? Will it be more complicated or simpler?

“It is unworthy of excellent men to lose hours like slaves in the labor of calculation which could be relegated to anyone else if machines were used.”
— Gottfried Leibniz
Let us calculate. First we calculate the partial derivatives – and they look really awful:
(5) 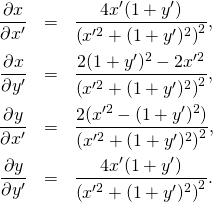
Then we compute ![]() and express it in terms of
and express it in terms of ![]() :
:
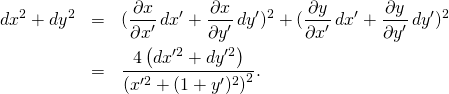
Certainly it is not a very simple formula.
Then we calculate the denominator of (4) and express it in terms of ![]() :
:
(6) ![]()
Also not very simple. But when we calculate the whole expression – a miracle happens:
(7) ![]()
(8) ![]()

Beautiful!
Why is it so that, after quite messy calculations, we arrive, at the end, at a very simple and beautiful end result? Probably the answer is that the end result must be invariant with respect to the very simple group, namely SL(2,R). So it must be simple. And it comes out even simpler than we would expect.
Next we need to exploit this simplicity …




Thanks!
Thanks.
Hi, how all these changes, if the radius of the disk is not 1, rather say L? Will there be just a factor of L^2 on both the half-plane and the Poincare disk metric?