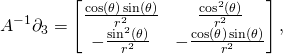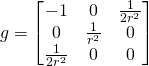The discussion in this post applies to Riemannian metrics on Lie groups in general, but we will concentrate
on just one case in hand: SL(2,R). Let ![]() be a Lie group. Vectors tangent to paths in
be a Lie group. Vectors tangent to paths in ![]() at identity
at identity ![]() form the Lie algebra of the group. Usually it is denoted by
form the Lie algebra of the group. Usually it is denoted by ![]() That is a real linear space, endowed with the commutator. For matrix groups the Lie algebra is a space of matrices (for the group SL(2,R) its Lie algebra sl(2,R) consists of matrices of zero trace), and the commutator is realized as the commutator of matrices:
That is a real linear space, endowed with the commutator. For matrix groups the Lie algebra is a space of matrices (for the group SL(2,R) its Lie algebra sl(2,R) consists of matrices of zero trace), and the commutator is realized as the commutator of matrices: ![]()
Suppose we have scalar product ![]() defined on the Lie algebra. For instance, if
defined on the Lie algebra. For instance, if ![]() are matrices, we may try to define
are matrices, we may try to define ![]() . That is a possible natural definition, the scalar product so defined is automatically symmetric. But it is not always nondegenerate, so one needs to be careful. When we have scalar product at identity, we can use group multiplication to propagate it to the whole group space by left translations:
. That is a possible natural definition, the scalar product so defined is automatically symmetric. But it is not always nondegenerate, so one needs to be careful. When we have scalar product at identity, we can use group multiplication to propagate it to the whole group space by left translations:
(1) ![]()
if ![]() are tangents to paths at
are tangents to paths at ![]() .
.
Notice that we are multiplying tangent vectors by group elements. For matrix groups that is easy, we simply multiply matrices. For more general groups is is understood that if ![]() is tangent to the path
is tangent to the path ![]() , then
, then ![]() is tangent to
is tangent to ![]()
The scalar product defined everywhere by Eq. (1) has automatically the property of being left-invariant:
(2) ![]()
The above equation needs explanation, its meaning follows from the context. On the left hand side we have scalar product. So, it is probably calculated at a certain point. We need to give this point some name. The symbol ![]() is used in the formula itself for the shift, so let us choose
is used in the formula itself for the shift, so let us choose ![]() . So, we specify the left hand side to mean
. So, we specify the left hand side to mean
![]()
Now, if ![]() is tangent at
is tangent at ![]() , then
, then ![]() itself must be tangent at
itself must be tangent at ![]() So, the complete formula should be:
So, the complete formula should be:
(3) ![]()
That is supposed to hold for any ![]() in the group. How do we prove it? We use the definition (1). The left hand side becomes
in the group. How do we prove it? We use the definition (1). The left hand side becomes
(4) ![]()
The right hand side becomes
(5) ![]()
The left and right hand sides equal because of the associativity of multiplication: ![]()
In a similar way we can propagate the scalar product from the Lie algebra to the whole group by right shifts. The so obtained scalar product (aka Riemannian metric) is then right-invariant. But these two Riemannian metrics in general will be different. Let us check under which conditions they would coincide? In order to coincide we would have to have:
![]()
for all ![]() tangent at
tangent at ![]() Denoting
Denoting ![]() we would have to have
we would have to have
![]()
for all ![]() in the Lie algebra. In other words: the scalar product at the identity would have to be Ad-invariant. We recall that “Ad” denotes the adjoint representation of the group on its Lie algebra defined as
in the Lie algebra. In other words: the scalar product at the identity would have to be Ad-invariant. We recall that “Ad” denotes the adjoint representation of the group on its Lie algebra defined as
![]()
The metric we have defined using trace
![]()
has this property because of the general property of the trace ![]() . But we could easily start with a different scalar product. Each scalar product give rise to different geodesics, different curvature. The group endowed with bi-invariant metric is, so to say, maximally “round”.
. But we could easily start with a different scalar product. Each scalar product give rise to different geodesics, different curvature. The group endowed with bi-invariant metric is, so to say, maximally “round”.
When metric is left (or right) invariant, that means that the group universe looks the same way from every point – it is “homogeneous”. But when it is also bi-invariant, that means that at every point it looks maximally the same in all directions – that is it has its natural “isotropy” property.