In the last post – Asymmetric Spinning Top – The Hardest Concept To Grasp In Physics – we have started grasping the hardest concept in physics – the asymmetric spinning top. And why asymmetric? Because symmetric tops are not that hard. Asymmetric are as hard as a diamond. Or harder. I have used a quote from Forbes magazine article This Is The Hardest Concept To Grasp In Physics (Hint: It’s Not Relativity). Here is what we find there that concerns directly our problem:
A friend recently pointed out to me this video of a T-handle spinning at zero gravity in the International Space Station, which provides an even more striking demonstration of the tennis racket theorem.
The so called “tennis racket theorem” is, in fact, a poor man explanation of the amazing phenomenon. The author of the Forbes’ article continues:
The T-handle is initially spun about the principal axis with intermediate moment of inertia, which is not stable. The result is that the axis reverses repeatedly. This particular behavior has recently been dubbed the “Dzhanibekov effect” after the Soviet cosmonaut Vladimir Dzhanibekov, who demonstrated it in space in 1985 (though the relevant physics has been understood at least since the work of Euler in the mid-18th century).
That is very very bad! It is cheating. Why? Because from the fact that something is unstable it does not follow in the least that the axis reverses repeatedly. About “the relevant physics has been understood at least since the work of Euler in the mid-18th century” I would say this: the relevant physics was known, but the phenomenon was not understood.
Then we have
This gives me another opportunity to reflect on some of the headaches associated with understanding the physics of spinning tops. There’s no torque acting on the T-handle, so its angular momentum ought to be fixed. How can this be reconciled with the fact that the axis of rotation is repeatedly flipping? The answer is that it flips in the top’s own frame of reference (which is not inertial). If you examine the video carefully you can see that, with respect to you as an inertial observer, the T-handle is spinning in the same direction before and after the flip!
Again totally misleading piece! “The answer is that it flips in the top’s own frame of reference (which is not inertial).“? What? What we see is that it flips in the laboratory frame of reference, which is inertial!
Very bad! Evidently the subject is too hard for the author of the article in Forbes. The same way as it is too hard for the authors of the Wikipedia entry Tennis racket theorem, which does not explain the observed phenomenon in the least. It just repeats the old observation known since at least 1897:
From Klein, Sommerfeld, Über die Theorie des Kreisels, 1897, p. 131
Racket definition, a loud noise or clamor, especially of a disturbing or confusing kind
Indeed! Never, never, never rely on Wikipedia. Always check sources, and sources of the sources (unless, of course, you know what you are doing – “And Jesus beheld a man working on the Sabbath, and He said to him, `Man, if you know what you do, you are blessed, for you break not The Law in the spirit; but if you know not, you are accursed and a transgressor of The Law.”, The Gospel of Nazarens, Ed. by Aklan Wauters and Rick Van Wyhe, Essen Vision Books , 1997)
We need to clear the path that we have started yesterday – using our own snowplows.
We will do it trying to follow the guidelines from How to Critique Artwork.
How to Critique Artwork
Here is our artwork – the same theme as in the previous post, though more elaborate, and colors are different
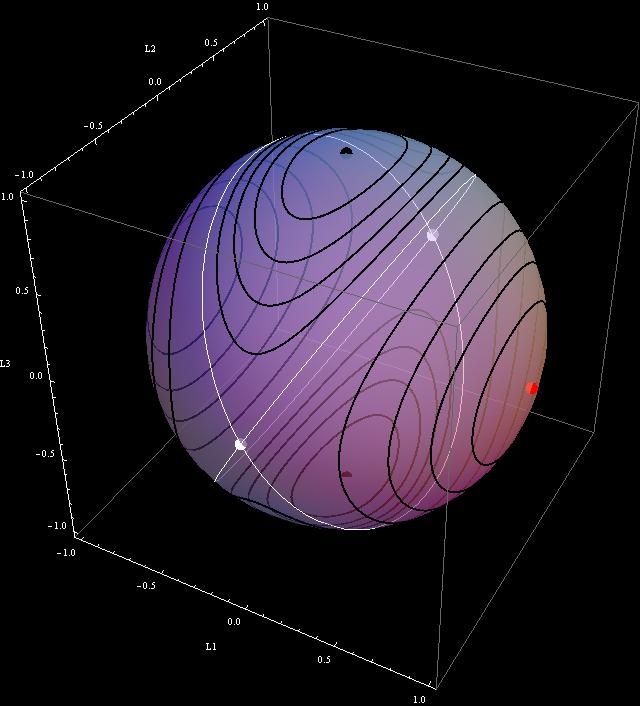
1. Describe what you see. This is the objective portion of the art critique. It involves a technical description-nothing more. It should include things like:
Artist’s name
Title of work
Type of artwork
Subject of the painting (scene)
Objects in the painting
First impression––note the characteristics of the artwork that first jump out at you
Colors used
Shapes, lines and texture
Light saturation
Sensory qualities––identify the predominant mood and visual effect.
Artist’s name: Mathematica
Title of work: Poinsot’s ellipsoid
Well, we have sphere rather than ellipsoid, but artists have some freedom…
Type of artwork: Parametric plots
Subject of the painting (scene): Landscape on the surface of constant angular momentum.
Objects in the painting: semi-transparent sphere, 6 points (two red, two white, two black), 16 black closed curves, 4 white half-circles
First impression––note the characteristics of the artwork that first jump out at you Hmmm… Looks like it would be better to draw more of these curves. Then we would perhaps see how they become points, and what happens to them when they are getting bigger and bigger.
Colors used: the sphere is light gray, other colors, mentioned already above, are far from being “subtle”
Shapes, lines and texture: The curves are intersections of the sphere with ellipsoids of different sizes. They look simple, but their mathematical expressions are not simple at all. Otherwise Wikipedia would tell us what they are.
Light saturation: poor. Cheap black background.
Sensory qualities––identify the predominant mood and visual effect: triggers curiosity, what it is about?
3
Interpret the artwork.
Now we are onto something. Reading about DaVinci, The Last Supper and Judas and Jesus we learn that
The life-model for the painting of the figure of Jesus was chosen first. When it was decided that DaVinci would paint this great picture, hundreds and hundreds of young men were carefully viewed in an endeavor to find a face and personality exhibiting innocence and beauty, free from the scars and signs of dissipation caused by sin.
Finally, after weeks of laborious searching, a young man nineteen years of age was selected as a model for the portrayal of Christ.
It was similar with our picture. There is an infinite number of rigid bodies. We want our to be asymmetric. But that is not of a much help. What we want is to have a rigid body that is “the best” for exhibiting the Dzhanibekov effect behavior. After weeks of laborious searching I have selected a rigid body with Principal Moments of Inertia:
(1) 
Every artist knows that the principal moments of inertia can not be arbitrary. They must be positive, that’s for sure. But they always have to satisfy the inequalities that the sum of any two of them is greater or equal than the third one. In our case, we decided always order them in increasing order: 
That means that we must have 
The two other inequalities are satisfied automatically. But we have chosen 
That means, in fact, that our model is essentially two-dimensional. That is it is similar to the T-handle fr4om the video. The letter T is, in principle, two-dimensional.
To prove that this is the best model for our scene needs, of course, a proof. Perhaps I will provide it at some later time. For now we have cleared a little bit of our path. More snow will be removed in the next post.
