Let me recall the particular trajectory that we are discussing. In fact the particular part of this particular trajectory where the flip occurs.
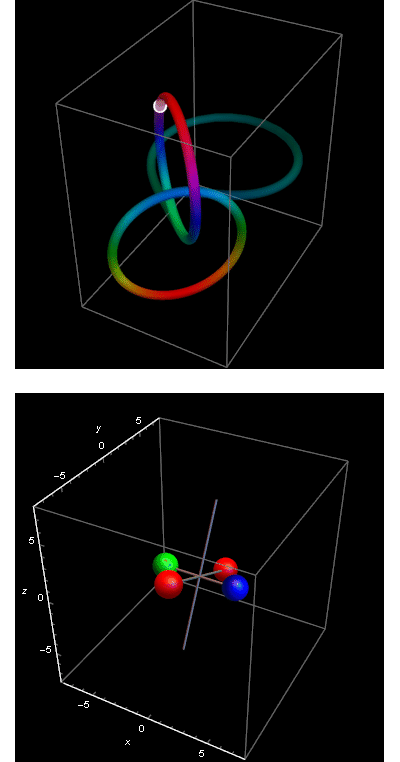
Click on the image to open gif animation. It will take time to load as it is 2.5 MB.
The flip is much like one of these flips that Russian cosmonaut Dzhanibekov observed in zero gravity, and was very much perplexed by the phenomenon.
We are investigating the jungle of math that we have to apply in order to simulate such a behavior of an ideal Platonic rigid body. At present we are analyzing the special conditions when only one flip happens. Apart of a rather short (as compared to eternity) period of time when the flip occurs, the body rotates uniformly about its middle axis. Its trajectory in the rotation group, represented by quaternions of unit norm, follows a circle. One circle before flip, another circle after the flip.
In this note I am taking a close look at these two circles. Can we find their exact coordinate representation in 3D after stereographic projection?
Yes, we can, and we will do it now.
We use the formulas from Meeting with remarkable circles.
For the body of our choice, with moments of inertia ![]() and on the trajectory where
and on the trajectory where ![]() the constants that enter the solution have values
the constants that enter the solution have values
(1) 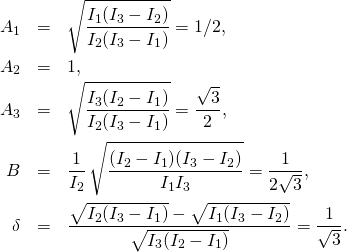
In the solution of the Euler’s equations we have functions ![]() and
and ![]()
(2) 
with ![]()
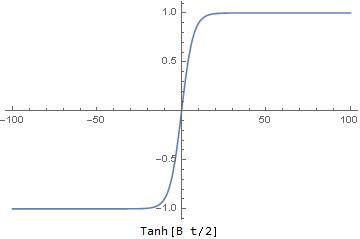
Here are the plots of these functions:

For ![]() we have
we have ![]() smaller than
smaller than ![]() and for
and for ![]() smaller than
smaller than ![]() We can consider it being zero for all practical purposes.
We can consider it being zero for all practical purposes.
As for ![]() it becomes practically constant and equal 1 for
it becomes practically constant and equal 1 for ![]() and
and ![]() for
for ![]()
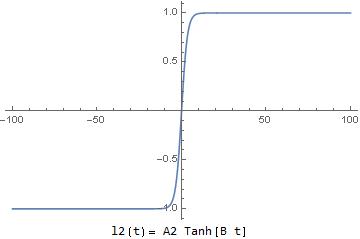
We then have the function ![]()
(3) ![]()
Again for all practical purposes for ![]() we have
we have
(4) ![]()
and for ![]()
(5) ![]()
Let us substitute these formulas into the solution for ![]()
(6) 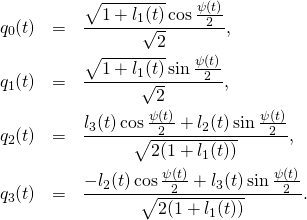
We obtain
(7) 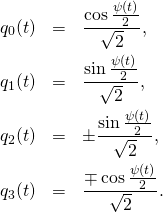
The upper signs concern ![]() the lower signs concern
the lower signs concern ![]()
In stereographic projection we are plotting ![]() divided by
divided by ![]() We see that the “future circle” is in the plane
We see that the “future circle” is in the plane ![]() while the past circle in the orthogonal plane
while the past circle in the orthogonal plane ![]()
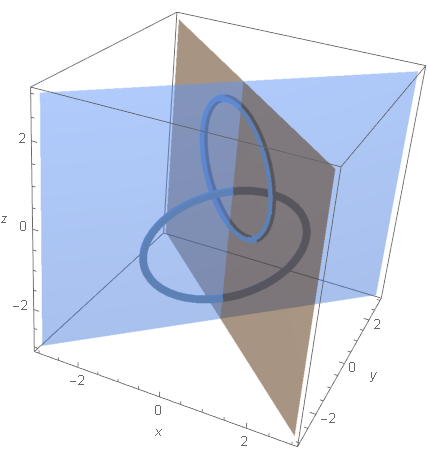
I did my geometric exercises and I have found that “the future circle” has origin at ![]() while “the past circle” has the origin at
while “the past circle” has the origin at ![]() Both circles have radius
Both circles have radius ![]()
So, we have complete information about these “circles of  eternal return”.
eternal return”.
One more comment: in Another geodesic line I was showing what I thought was a subtle structure of the trajectory approaching the circle:

But now I know that it was a numerical artefact. As noticed in today’s post, for ![]() computer will see only one line, no fine structure. To be sure I asked my computer to take more points on the plot (100000 instead of 10000) and all the fine structure disappeared.
computer will see only one line, no fine structure. To be sure I asked my computer to take more points on the plot (100000 instead of 10000) and all the fine structure disappeared.