In Geodesics on upper half-plane factory direct we used the Christoffel symbols and identified geodesics on the upper half plane endowed with the hyperbolic geometry metric. The formulas for Christoffel symbols contain derivatives of the metric tensor components:
(1) ![]()
From these connection coefficients one constructs the Riemann curvature tensor. Let us take the expression from Wikipedia:
(2) ![]()
From its construction several symmetries follow, so that only ![]() really independent components remain. For
really independent components remain. For ![]() one has to calculate 20 components. But for
one has to calculate 20 components. But for ![]() it is only one. But even this one, why should we calculate it? We better listen to Leibniz.
it is only one. But even this one, why should we calculate it? We better listen to Leibniz.
“It is unworthy of excellent men to lose hours like slaves in the labour of calculation which could safely be relegated to anyone else if machines were used.“
Nowadays software does all that. Right now I ma using Mathematica, so I type
riemann = Simplify[Table[
D[christ[[i, j, l]], coord[[k]] ] –
D[christ[[i, j, k]], coord[[l]] ] +
Sum[christ[[s, j, l]] affine[[i, k, s]] –
christ[[s, j, k]] affine[[i, l, s]],
{s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}, {l, 1, n}] ]
With the result that
(3) 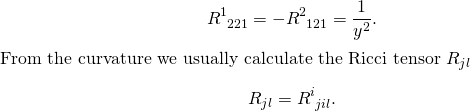
The Ricci tensor is obtained by contraction (summation) over two indices of the Riemann tensor. The Ricci tensor is always automatically symmetric. In our case we get that Ricci is simply the negative of the metric
(4) ![]()
Spaces in which this happens are known under a special name: Einstein spaces (or “Einstein manifolds“).
From Ricci tensor by contraction with the inverse metric one calculates the scalar curvature. In our case the result is -2:
(5) ![]()
While Riemann and Ricci are “tensors”, they may have different components in different coordinate systems, the scalar curvature is an invariant. Its value is independent of the coordinates. In our case the result -2 would be the same if we have calculated it with the coordinates and metric that we have used on the Poincare disk.
From two dimensions of the Poincare disk and the upper half-plane we will now move to three-dimensions of the group SL(2,R) itself.
Below is the view of the Mathematica notebook doing the calculations described in this post.