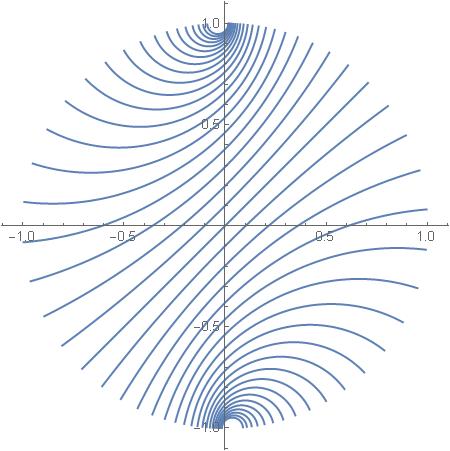
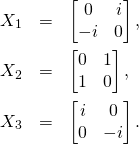Category: Hyperbolic geometry

Hyperbolic geometry – Playing with parallels

Posted on by arkajad

In SU(1,1) straight lines on the disk we have seen nice families of parallel straight lines in the hyperbolic geometry of the unit disk of the complex plane. Here is one such family:

Family of parallel straight lines

Let us recall how was it obtained. We start with a template straight line through the origin o at z=0..

Template straight line

Then we take one-parameter group of SU(1,1) transformations A_1(t) generated by X_1

(1)   \begin{equation*}X_1=\begin{bmatrix}0&i\\-i&0\end{bmatrix},\end{equation*}

(2)   \begin{equation*}A_1(t)= \exp(tX_1)=\begin{bmatrix}\cosh(t)&i\sinh(t)\\-i\sinh(t)&\cosh(t)\end{bmatrix}.\end{equation*}

We apply transformations A_1(t) to our template straight line (we use fractional linear transformations explained in previous posts), for several different values of t, and we obtain the family depicted above.

Let us take a particular case, with t=-0.4.

We have \sinh(-0.4)=-0.410752, \cosh(-0.4)=1.08107, therefore the point (x,0) on the template line is transformed into p(x) given by

(3)   \begin{equation*}p(x)=\frac{1.08107 x+0.410752 i}{1.08107-0.410752 x i}.\end{equation*}

The whole template line is transformed as follows

Template and one parallel

We obtain another straight line, parallel to the original one (as the two lines do not intersect). If we rotate this new line clockwise about the origin, at a certain point the two lines touch at z=1. That is the limit of being parallel. If we rotate further, then the two lines start to intersect.

Let us calculate the angle \phi that we need to use to reach the limit. We set x=1 in Eq. (3) and solve for \phi such that

(4)   \begin{equation*}e^{i\phi}=\frac{1.08107+0.410752 i}{1.08107-0.410752 i}.\end{equation*}

Solving this I am finding (in radians)

(5)   \begin{equation*}\phi=0.726204822741529.\end{equation*}

Our U(1) rotation group is defined by matrices

(6)   \begin{equation*}U(t)=\begin{bmatrix}e^{it}&0\\ 0&e^{-it}\end{bmatrix}.\end{equation*}

It acts on complex numbers by:

(7)   \begin{equation*}U(t):z\mapsto e^{-2it}z.\end{equation*}

Therefore in order to obtain the limiting line we need to apply U(\phi/2)

(8)   \begin{equation*}U(\phi/2)=\begin{bmatrix} 0.934799+0.355176 i & 0 \\ 0 & 0.934799-0.355176 i \end{bmatrix}\end{equation*}

The total transformation U(\phi/2)P(-0.4) that we will use is therefore

(9)   \begin{equation*}\begin{bmatrix} 1.01059\, +0.383971 i & 0.145889\, -0.383971 i \\ 0.145889\, +0.383971 i & 1.01059\, -0.383971 i \\ \end{bmatrix}.\end{equation*}

Acting on the point x on the real axis it produces a point p(x) in the disk

(10)   \begin{equation*}p(x)=\frac{(1.01059\, -0.383971 i) x+(0.145889\, +0.383971 i)}{(0.145889\, -0.383971 i) x+(1.01059\, +0.383971 i)}\end{equation*}

    \[=\frac{(1.7477 + 4.43167 x + 1.7477 x^2)+(1.9679 - 3.93579 x + 1.9679 x^2)i}{x^2+6.92707}.\]

The real part, 1.7477 + 4.43167 x + 1.7477 x^2 vanishes for x=-0.488459, The imaginary part has, for this x the value 0.608442. That means that at z=0.608442 i the limiting line crosses the vertical imaginary axis.

Template and the limiting parallel

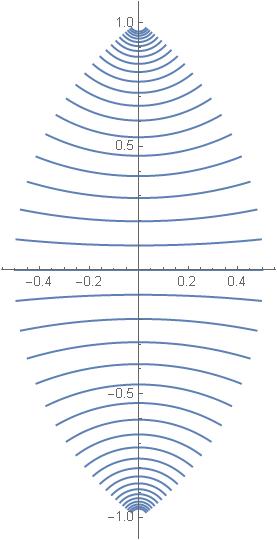
We could easily repeat the above reasoning applied, this time, to the left point z=-1. We would get the second limiting line. The two lines cross at z_0=0.608442 i, as shown below:

Template and two limiting parallels

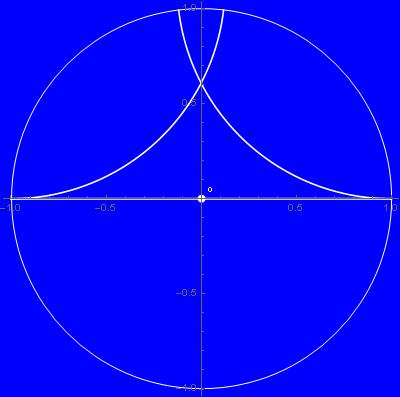
We will continue our adventure in the next post. We will produce there this image of parallel lines – the Angel of Geometry

Template and parallels through one common point.

SU(1,1) preserves angles

Posted on by arkajad

In the last post, SU(1,1) straight lines on the disk, we have seen families of straight lines of the hyperbolic geometry on the disk. Here is another family:

These lines are straight and they are parallel to each other, except that not in Euclidean geometry of the plane, but in the hyperbolic geometry that is based on constructions that are invariant with respect to SU(1,1) fractional linear transformations that we have met in previous notes.

These lines are obtained by applying SU(1,1) transformations to one straight line. Therefore they are not only all straight, but they all have the same length. This observation is not, however, very revealing, because, as we will see later, in the forthcoming notes, all these lines are of infinite length. The reason that they have infinite length is that they extend to the very ends of the disk universe.

In order to learn something about the length in the hyperbolic geometry of the disk let us take a segment of a straight line that is finite. I am taking the segment defined by y=0 and 1/2\leq x\leq 1/2. I apply to this segment transformations from the one-parameter group A_1(t) of SU(1,1) transformations defined in the previous post. Here is the result:

The right ends are on the trajectory of A_1(t) passing through the point (1/2,0). The one-parameter group A_1(t) leaves the vertical line invariant (even though it moves points on this line). Therefore the right ends are equidistant from the middle vertical straight line. But these points, even if they are in a constant distance from a straight line, are not on a straight line. This observation is related to the question asked by Bjab. In my reply I mentioned that straight lines of the hyperbolic geometry of the disk are segments of circles that meet the boundary at right angles. The pictures seem to support this property, but I did not give any proof of it, even a “baby proof”. It is now time to fill this hole.

We will show that transformations from SU(1,1) preserve angles. Of course they would certainly preserve “hyperbolic angles”, by definition of hyperbolic geometry, but here we will show that they preserve Euclidean angles. They do not preserve Euclidean lengths, but angles they do preserve! One says: they are conformal.

What would it mean that angles are preserved? Let us take a point z_0 and two curves \gamma_1(t), \gamma_2(t) such that \gamma_1(0)=\gamma_2(0)=z_0, that meet at some angle \alpha_0 at z_0. If A is a matrix in SU(1,1), it sends the point z_0 to a new point z_0', and it sends the curves \gamma_1 and \gamma_2 to \gamma_1' and \gamma_2'. The curves \gamma_1' and \gamma_2' meet at z_0' at some angle \alpha_0'. What we want to show is that \alpha_0'=\alpha_0.

First we are going to simplify our task by using what we already know.

We know that SU(1,1) acts on the disk transitively. We can always move the point z_0 to the origin z=0. If we are able to prove our statement for all SU(1,1) transformations and z_0=0, then it will immediately follow that the statement is true in general.

We know that every transformation from SU(1,1) can be decomposed into U(1) rotation U(\theta) and a positive matrix P(z). Rotations are just Euclidean rotations about the center of the disk. They evidently preserve Euclidean angles. It is therefore enough to consider P(z) transformations.

Let therefore \gamma_1(t), \gamma_2(t) be such that \gamma_1(0)=\gamma_2(0)=0. In coordinates \gamma_1(t) is described by functions z_1(t)=(x_1(t),y_1(t)),
while \gamma_2(t) is described by functions z_2(t)=(x_2(t),y_2(t)). Tangent vectors to \gamma_1 and \gamma_2 at z=0 have components \dot{\gamma}_1(0)=(\dot{x}_1(0),\dot{y}_1(0)) and \dot{\gamma}_2(0)=(\dot{x}_2(0),\dot{y}_2(0)) respectively. The angle \alpha_0 is determined by

    \[ \cos \alpha_0=\frac{\dot{\gamma}_1(0)\cdot\dot{\gamma}_2(0)}{|\dot{\gamma}_1(0)||\dot{\gamma}_2(0)|}.\]

Let us now take P(z), with z=x+iy

(1)   \begin{equation*} P(z)=\begin{bmatrix}\frac{1}{\sqrt{1-|z|^2}}&\frac{\bar{z}}{\sqrt{1-|z|^2}}\\ \frac{z}{\sqrt{1-|z|^2}}&\frac{1}{\sqrt{1-|z|^2}}\end{bmatrix}.\end{equation*}

It transforms z_1(t) into z_1'(t) given by

(2)   \begin{equation*}z_1'(t)=\frac{z_1(t)+z}{\bar{z}z_1(t)+1}.\end{equation*}

Now, we differentiate with respect to t at t=0 remembering that z_1(0)=0. We use the standard quotient rule,

even if here we apply it to a function with complex values. The result that I am getting is:

(3)   \begin{equation*}\dot{z}_1'(0)=(1-|z|^2)\dot{z}_1(0).\end{equation*}

Similarly we obtain

(4)   \begin{equation*}\dot{z}_2'(0)=(1-|z|^2)\dot{z}_2(0).\end{equation*}

Therefore the components of the transformed vectors are equal to the components of the original vectors multiplied by the same positive factor. It follows that the angles between them are the same.

Of course the proof above is a baby proof. Adults know that any holomorphic transformation preserves angles on the complex plane. Easy proof can be found here.

SU(1,1) straight lines on the disk

Posted on by arkajad

As we have learned in SU(1,1) action on the disk, the matrix Lie group SU(1,1) acts transitively, by linear fractional transformations, on the unit disk D in the complex plane. The disk D is a homogeneous space for SU(1,1). The points of the disk can be considered as orbits of the U(1) subgroup of SU(1,1), acting on SU(1,1) from the right. In Getting hyperbolic we have already seen the actions of three one-parameter subgroups of SU(1,1), let us call them A_1(t),A_2(t),A_3(t). They come from exponentiation of three different generators X_1,X_2,X_3, elements of the Lie algebra of the group:

(1)   \begin{eqnarray*} X_1&=&\begin{bmatrix}0&i\\-i&0\end{bmatrix},\\ X_2&=&\begin{bmatrix}0&1\\1&0\end{bmatrix},\\ X_3&=&\begin{bmatrix}i&0\\0&-i\end{bmatrix}. \end{eqnarray*}

(2)   \begin{eqnarray*} A_1(t)&=& \exp(tX_1)=\begin{bmatrix}\cosh(t)&i\sinh(t)\\-i\sinh(t)&\cosh(t)\end{bmatrix},\\ A_2(t)&=& \exp(tX_2)=\begin{bmatrix}\cosh(t)&\sinh(t)\\ \sinh(t)&\cosh(t)\end{bmatrix},\\ A_3(t)&=& \exp(tX_3)=\begin{bmatrix}e^{it}&0\\ 0&e^{-it}\end{bmatrix}. \end{eqnarray*}

Streamlines for these three one-parameter transformation groups (and they have been derived in Getting hyperbolic) acting on the disk are on the pictures below.


Now that we have transitive action of SU(1,1) on the disk, we can implement the Erlangen program and study disk’s geometry by analyzing properties of invariants of this action. We call SU(1,1) the symmetry group of the disk.

We will start with looking for a reasonable definition of “straight lines”. First let us consider the most reasonable candidate for a straight line of the disk’s geometry, the vertical line through the center o of the disk:

Straight line candidate

Notice that it is the trajectory of A_1(t) that passes through the origin o.

It is a perfect candidate for a straight line. For when you start vertically, there is no reason to deflect to the right or to the left if you are going to move “straight”. Thus we take it as our primary straight line.

Of course arguing that “there is no reason to deflect” does not sound very rigorous. It is, I agree, a “baby talk“.

But in this case it is enough. I could have argued in a different way, in an “adult way“, by quoting from the second volume of Foundations of Differential Geometry by Kobayashi and Nomizu:

But the end result would be the same. The vertical line is a “geodesic”, is a “straight line”.

According to the Erlangen program for geometry, initiated by Felix, Klein, in our case we will call it “hyperbolic geometry” or “Lobachevsky-Bolyai geometry“, every transformation from the symmetry group transforms straight line into straight line. So, here I am using
A_2(t) for t going from -2, to +2, step 0.1, to get a family of 40 other straight lines of our geometry:

Family of parallel straight lines

They are all images of our vertical straight line. Therefore, even if they do not look very straight, they are, by definition.

But the one-parameter group A_3(t) is also a symmetry group of our geometry. Transformations from this group rotate around the center o. So rotations of our straight line are also straight lines. Here is a family of straight lines obtained from the horizontal line by applying the transformations A_1(t).

Family of parallel straight lines

Notice that these straight lines are as long as they can only be, and they do not intersect. Therefore, by definition, they are all parallel.


We will continue our adventure in the following posts. Once we are here, we must certainly touch the Fifth Euclid’s postulate – one that is violated in our geometry.