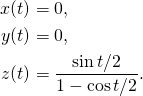The recollections in the last post were incomplete. So, here is the continuation.
We have derived the property
On the other hand we stressed the fact that
(2) ![]()
is the rotation matrix that describes the rotation about the axis in the direction ![]() by an angle
by an angle ![]() .
.
From these two properties we can deduce the third one:
To deduce this last property we use the fact that for any ![]() and any invertible
and any invertible ![]() we have:
we have:
![]()
The proof of the above follows by expanding ![]() as a power series, and noticing that
as a power series, and noticing that ![]()
I will use spin equivalent of Eq. (3) when explaining how exactly I got the two images from the last post that I am showing again below:
The advantage in using Eq. (3) is that it may be easy to calculate the exponential ![]() but not so easy the exponential
but not so easy the exponential ![]()
Our aim is to draw trajectories in the rotation group ![]() made by the asymmetric top spinning about its largest moment of inertia axis, which in our setting is the third axis. As the rotation group
made by the asymmetric top spinning about its largest moment of inertia axis, which in our setting is the third axis. As the rotation group ![]() is not very graphics friendly, we are using the double covering group
is not very graphics friendly, we are using the double covering group ![]() or, equivalently, the group of unit quaternions. We then use stereographic projection to project trajectories from the 3-dimensional sphere
or, equivalently, the group of unit quaternions. We then use stereographic projection to project trajectories from the 3-dimensional sphere ![]() to 3-dimensional Euclidean space
to 3-dimensional Euclidean space ![]()
But first things first. Before doing anything more we first have to translate the above properties into the language of ![]() Therefore another recollection is necessary at this point. In Pauli, rotations and quaternions we have defined three spin matrices:
Therefore another recollection is necessary at this point. In Pauli, rotations and quaternions we have defined three spin matrices:
(4) ![]()
In Putting a spin on mistakes we have explained that we have the map ![]() that associates rotation matrix
that associates rotation matrix ![]() to every matrix
to every matrix ![]() in such a way that for every vector
in such a way that for every vector ![]() we have
we have
(5) ![]()
It follows immediately from the above formula that ![]() is a group homomorphism, that is we have
is a group homomorphism, that is we have
(6) ![]()
At the end of Putting a spin on mistakes we have arrived at the formula:
(7) ![]()
which tells us that the matrix ![]() defined as
defined as
(8) ![]()
describes the rotation about the direction of the unit vector ![]() by the angle
by the angle ![]() at the
at the ![]() level.
level.
The map ![]() is 2:1. We have
is 2:1. We have ![]() Matrices
Matrices ![]() and
and ![]() implement the same rotation. When
implement the same rotation. When ![]() changes from
changes from ![]() to
to ![]() the matrix
the matrix ![]() in Eq. (7) describes the full
in Eq. (7) describes the full ![]() turn, but the matrix
turn, but the matrix ![]() becomes
becomes ![]() rather than
rather than ![]() . We need to make
. We need to make ![]() rotation at the
rotation at the ![]() vector level to have
vector level to have ![]() rotation at the spin level. That is described by
rotation at the spin level. That is described by ![]() in the exponential in Eq. (7).
in the exponential in Eq. (7).
At the spin level we then obtain the following analogue of Eq. (\ref:rqr}):
Now we can finally look back at the images of trajectories. In Seeing spin like an artist we noticed that rotation about the z-axis is described by the matrix
(10) ![]()
while rotation by the angle ![]() about y-axis is described by the matrix
about y-axis is described by the matrix
(11) 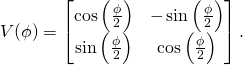
![]() describes uniform rotation of the top about its z-axis, when the z-axis of the top and of the laboratory frame are aligned. As observed in Towards the road less traveled with spin that is not an interested path for drawing. To make the path more interesting we tilt the laboratory frame. To this end we use, for instance, the matrix
describes uniform rotation of the top about its z-axis, when the z-axis of the top and of the laboratory frame are aligned. As observed in Towards the road less traveled with spin that is not an interested path for drawing. To make the path more interesting we tilt the laboratory frame. To this end we use, for instance, the matrix ![]() with
with ![]()
(12) ![]()
Now the axis of rotation of the top is tilted by 30 degrees with respect to the z-axis of the laboratory frame. We get new path of the evolution in the group ![]()
(13) ![]()
From Eq. (1) in Chiromancy in the rotation group we can now calculate real parameters ![]() For a general matrix
For a general matrix ![]() the formulas are:
the formulas are:
(14) 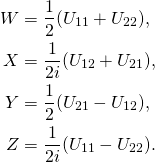
In our particular case we get:
(15) 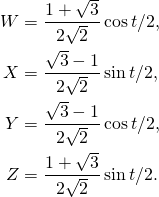
We then get rather awfully looking the parametric formulas for the stereographic projection:
(16) 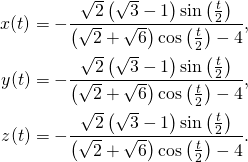
The result (running ![]() from
from ![]() to
to ![]() ) is not very interesting – just a circle:
) is not very interesting – just a circle:
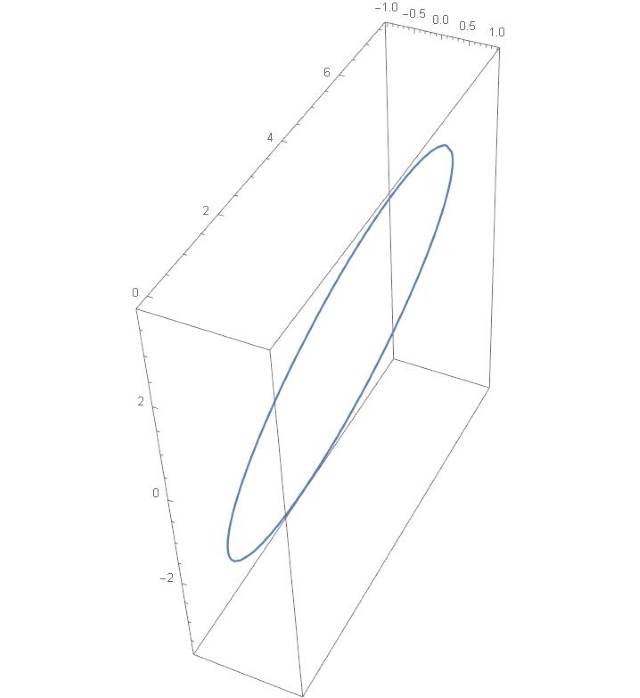
It is better than the straight line with a non tilted top, but not a big deal. But the next thing we want to do is to rotate the tilt axis in the (x,y) plane, that is about the ![]() -axis of the laboratory. If we want to rotate by an angle
-axis of the laboratory. If we want to rotate by an angle ![]() we should replace
we should replace ![]() by
by ![]() – according to Eq. (9). That is we should look at the trajectory:
– according to Eq. (9). That is we should look at the trajectory:
![]()
Now, ![]() Since anyway we are are going to run with
Since anyway we are are going to run with ![]() through the whole
through the whole ![]() interval, we can as well use
interval, we can as well use ![]() instead of
instead of ![]() Therefore we can draw
Therefore we can draw
![]()
We can calculate ![]() and then
and then ![]() Here are the results from my Mathematica code:
Here are the results from my Mathematica code:
(17) 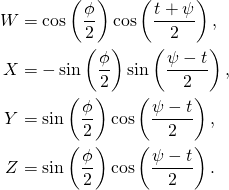
(18) 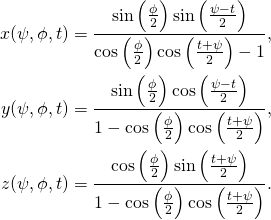
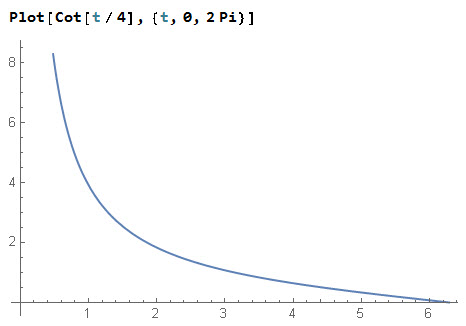
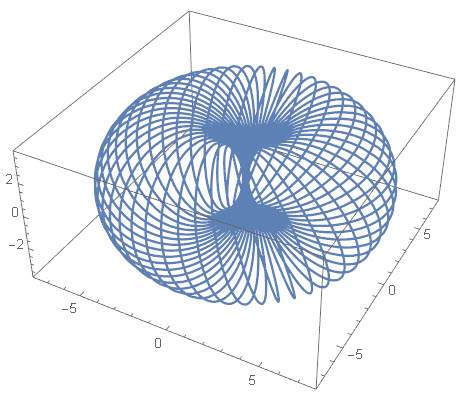
And here is the resulting of plotting 30 such circles, each for ![]() with
with ![]() increasing from 0 t0 180 degrees, every 6 degrees:
increasing from 0 t0 180 degrees, every 6 degrees:
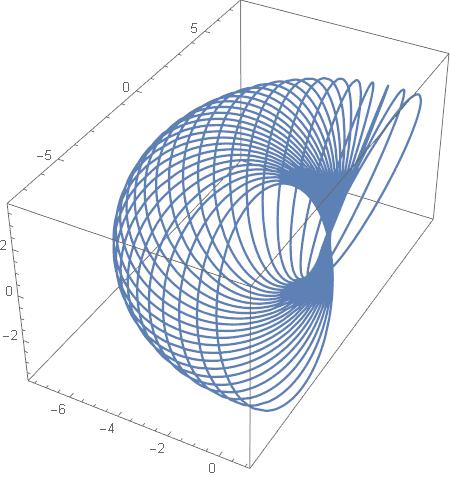
It looks like half of a torus. With ![]() we get another, larger torus …
we get another, larger torus …
In the next posts we will disturb the motion of the top to see what kind of trajectories we will be getting then.